opencv--使用直方图找谷底进行确定分割阈值

直方图原理就不说了，大家自行百度

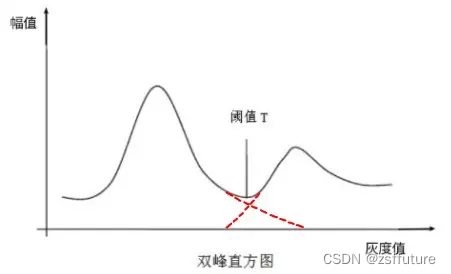
直方图可以帮助分析图像中的灰度变化，进而帮助确定最优二值化的灰度阈值（threshold level）。如果物体与背景的灰度值对比明显，此时灰度直方图就会包含双峰（bimodal histogram），即直方图中一般会有两个峰值，分别为图像的前景和背景。

前景使得某个灰度区间的灰度值的数量急剧增加，就会产生一个峰值，同理背景会使另一个灰度区间的灰度值的数量急剧增加，就产生另外一个峰值，两峰间的谷底对应于物体边缘附近相对较少数目的像素点。

这两个峰值之间的最小值一般就是最优二值化的分界点，通过这个分界点可以把前景和背景很好地分割开来。

有时这两个峰值会有部分重叠，即左侧峰值的下降部分和右侧峰值的上升部分存在叠加。通常可以把自然界的信号看做高斯信号，即一个峰值对应一个高斯信号，当直方图中的两个高斯信号在某个灰度区域叠加的时候，其叠加区就形成了一个圆滑的谷底，就很难找到一个确切的位置（最优二值化的灰度值）把这两个峰值分开。

float calculateThreshold(cv::Mat& img)
{
    cv::Mat temp = img.clone();
    
    // 计算直方图
    cv::Mat hist;
    int histSize = 256;  // 直方图尺寸
    float range[] = { 0, 256 };  // 像素值范围
    const float* ranges[] = { range };
    cv::calcHist(&img, 1, nullptr, cv::Mat(), hist, 1, &histSize, ranges);
    /*for (int i = 0; i  nextValue && currentValue>0.005)) {
            std::cout