离散化及模板详解

⭐写在前面的话：本系列文章旨在复习算法刷题中常用的基础算法与数据结构，配以详细的图例解释，总结相应的代码模板，同时结合例题以达到最佳的学习效果。本专栏面向算法零基础但有一定的C++基础的学习者。若C++基础不牢固，可参考：10min快速回顾C++语法，进行语法复习。

文章目录

• 离散化
• • • 基本思想
    • 算法思路
    • 模板
    • 例题：区间和
    • • 题目分析
      • code

        离散化

        基本思想

        首先，离散化是指数值域非常大，例如 1 − 1 0 6 1-10^6 1−106，但是个数相对较少,例如只有 1 0 3 10^3 103个, 但在我们的程序中需要通过这些数值作为下标,且依赖的是这些数值之间的顺序关系（当然通常这些数是有序的）。如果为了这 1 0 3 10^3 103个数而开一个 1 0 6 10^6 106的数组过于浪费空间，因此我们可以采用离散化的方法，将这些数映射到 0 − 1 0 3 0-10^3 0−103上，这个过程就叫做离散化。

        注意：这里的映射数字指的是元素的下标数字，而非元素本身的数值。

        算法思路

        对于有序数组进行映射，其基本思路如下：

        

        针对可能存在的两个问题，有以下的解决方法：

        1.数组中可能存在重复元素 ==> 对数组进行去重

        常见写法：用cpp中的库函数来实现。

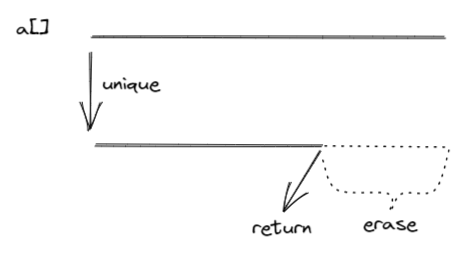
        unique函数：将数组中的元素去重，并且返回去重后数组的尾端点。

        

        vector alls; // 存储所有待离散化的值
        sort(alls.begin(), alls.end()); // 将所有值排序
        alls.erase(unique(alls.begin(), alls.end()), alls.end());   // 去掉重复元素
        

        2.如何算出x离散化后的值 ==> 用二分法

        int find(int x) // 找到第一个大于等于x的位置
        {
            int l = 0, r = alls.size() - 1;
            while (l > 1;
                if (alls[mid] >= x) r = mid;
                else l = mid + 1;
            }
            // 映射到1, 2, ...n
            // 不加1的话是从0开始映射。
            return r + 1;
        }
        

        模板

        vector alls; // 存储所有待离散化的值
        sort(alls.begin(), alls.end()); // 将所有值排序
        alls.erase(unique(alls.begin(), alls.end()), alls.end());   // 去掉重复元素
        // 二分求出x对应的离散化的值
        int find(int x) // 找到第一个大于等于x的位置
        {
            int l = 0, r = alls.size() - 1;
            while (l > 1;
                if (alls[mid] >= x) r = mid;
                else l = mid + 1;
            }
            // 映射到1, 2, ...n
            // 不加1的话是从0开始映射。
            return r + 1;
        }
        

        例题：区间和

        假定有一个无限长的数轴，数轴上每个坐标上的数都是 0。

        现在，我们首先进行 n 次操作，每次操作将某一位置 x 上的数加c。

        接下来，进行 m 次询问，每个询问包含两个整数 l 和 r，你需要求出在区间 [l,r]之间的所有数的和。

        输入格式

        第一行包含两个整数 n 和 m。

        接下来 n 行，每行包含两个整数 x 和 c。

        再接下来 m 行，每行包含两个整数 l 和 r。

        输出格式

        共 m 行，每行输出一个询问中所求的区间内数字和。

        数据范围

        − 1 0 9 ≤ x ≤ 1 0 9 −10^9≤x≤10^9 −109≤x≤109,

        1 ≤ n , m ≤ 1 0 5 1≤n,m≤10^5 1≤n,m≤105,

        − 1 0 9 ≤ l ≤ r ≤ 1 0 9 −10^9≤l≤r≤10^9 −109≤l≤r≤109,

        − 10000 ≤ c ≤ 10000 −10000≤c≤10000 −10000≤c≤10000

        输入样例：

        3 3
        1 2
        3 6
        7 5
        1 3
        4 6
        7 8
        

        输出样例：

        8
        0
        5
        

        题目分析

        数据范围很大，因此不能用哈希表，并且数轴上的数字是离散的，整体是稀疏的，我们可以采用离散化的方式进行映射。

        • add : 保存真实的下标和相应的值
        • alls : 用来保存真实的下标和映射的下标的关系
        • query : 用来保存查询的左右两个端点
        • a : 保存映射的坐标所对应的值
        • s: 保存映射的坐标所对应的值的前缀和

          第一步: 输入数轴上所对应的值

          for(int i=0;i
          	int index,x; cin>index>>x;
          	add.push_back({index,x});//index 是我们真实的下标 x是数值
          	alls.push_back(index);// 将真实的下标和我们想象的坐标建立映射关系
          }
          

          第二步: 输入我们的查询的区间

          for(int i=0;i
          		int l,r; cin>l>>r;
          		query.push_back({l,r});//保存查询的区间
          		
          		alls.push_back(l);
          		//将其左右端点也映射进来，目的是可以让我们在虚拟的映射表里找到，这对于我们后面的前缀和操作时是十分的方便的。
          		//如果当我们在虚拟的映射表里找的时候，如果没有找到左右端点，那么前缀和无法求。
          		alls.push_back(r);
          	}
          

          第三步: 将虚拟的坐标排序并去重

          为啥去重:

          是因为当我们输入

          3 5

          3 6

          即给数轴上3的点加5 再加 6时。此时我们的坐标映射表里有了两个3 3 但其实它们对应的是同一个坐标。故需要去重，排序。

           sort(alls.begin(), alls.end());//排序
           alls.erase(unique(alls), alls.end());//去重(坐标)
          

          第四步：根据真的坐标，来找到对应虚拟的坐标，将其位置加上其相对应的数值。

          根据真的坐标找其对应的映射的坐标，用二分来查找。

          int find(int x)
          {
          	int l=0,r=alls.size()-1;
          	while(l
          		int mid=l+r>1;
          		if(alls[mid]>=x) r=mid;
          		else l=mid+1;
          	}
          	return l+1;//  因为要求前缀和，故下标从1开始方便，不用额外的再处理边界。
          }
          for(int i=0;i
          		int x=find(add[i].first);
          		a[x]+=add[i].second;
          } 
          
          	int l=find(query[i].first),r=find(query[i].second);
          	cout
              int l = 0, r = alls.size() - 1;
              while(l > x >> c;
                  add.push_back({x, c});
                  
                  alls.push_back(x);
              }
              // 对左右边界输入
              for(int i = 0; i > l >> r;
                  query.push_back({l, r});
                  
                  alls.push_back(l);
                  alls.push_back(r);
                  
              }
              // 进行去重
              sort(alls.begin(), alls.end());
              alls.erase(unique(alls.begin(),alls.end()), alls.end());
              // 遍历add
              for(auto item : add)
              {
                  // 找到该值的位置
                  int x = find(item.first);
                  // 用数组存储该值，相当于在空数组上加上这个数字
                  a[x] += item.second;
              }
              // 前缀和数组
              for(int i = 1; i 
                  // 找到左右边界的位置
                  int l = find(item.first), r = find(item.second);
                  // 输出该段的和
                  cout 
              int j = 0;
              for(int i = 0; i