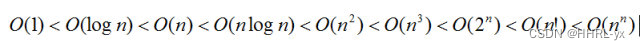算法基础1:复杂度和简单算法
目录
一.时间复杂度
1.概述
2.时间复杂度表达
3.简便计算时间复杂度
4.注意事项
二.简单算法
1.异或运算
(1)交换操作
(2)异或算法应用1
(3)异或算法应用2
2.插入排序
3.二分法
4.对数器
三.空间复杂度
1.概念
2.空间复杂度计算和表示
(1)计算步骤:
(2)空间复杂度的表示
3.示例代码
(1)空间复杂度O(1)
(2)空间复杂度O(n)
一.时间复杂度
1.概述
一个操作如果和样本的数据量没有关系,每次都是固定时间内完成的操作,叫做常数操作。
时间复杂度为一个算法流程中,常数操作数量的一个指标。常用0(读作big 0)来表示。具体来说,先要对一个算法流程非常熟悉,然后去写出这个算法流程中,发生了多少常数操作,进而总结出常数操作数量的表达式。在表达式中,只要高阶项,不要低阶项,也不要高阶项的系数,剩下的部分如果为f(N),那么时间复杂度为0(f(N))。
时间复杂度表示某个算法运行时间的趋势,可以大致评判程序的效率。 评价一个算法流程的好坏,先看时间复杂度的指标,然后再分析不同数据样本下的实际运行时间,也就是“常数项时间”。
2.时间复杂度表达
列出需要执行程序的次数,写成T(N)=aN²+bN+C的形式。此时,以存在的最高次项作为时间复杂度,因为N趋于无穷时,只有最高次项对结果的影响大。
例如:列出式子为aN³+bN+C,时间复杂度即为O(N³)。
具体的高阶低阶排行如下图:
如果阶数指标相同,无法通过常数项比较时间复杂度,只能通过实际跑代码区分。
3.简便计算时间复杂度
一般来说,最内层执行次数最多的语句就决定了整个算法的趋势,通常看最内层语句执行次数的规律即可。
4.注意事项
对于任何算法流程,估计时间复杂度O时,按照最差情况估计。
二.简单算法
1.异或运算
(1)交换操作
此时a和b必须拥有不相同的内存空间,因为同样的内存区域跟自己异或,会直接变成0。
void swap(int,a, int b)
{
a = a ^ b;
b = a ^ b;
a = a ^ b;
}
(2)异或算法应用1
问题:一个数组中,只有1个数出现奇数次,其他数均出现偶数次。求出现奇数次的这个数。
解法:定义一个eor = 0,将数组中所有数与其异或,异或出的eor即为解。因为异或运算同一批数,不管顺序如何,异或结果一样。所以等同于偶数次的数先异或。
原理:异或的交换律。
#include
#include
#include
using namespace std;
void solve(int num[]);
int main() {
//算法问题1:问题:一个数组中,只有1个数出现奇数次,其他数均出现偶数次。求出现奇数次的这个数
//解法:定义一个eor = 0,将数组中所有数与其异或,异或出的eor即为解。
int nums[] = { 1,2,1,2,1,3,2,1,2,3,3 };
solve(nums);
system("pause");
return 0;
}
void solve(int num[]) {
int eor = 0;
int len = sizeof(num) / sizeof(num[0]);
for (int i = 0; i