差分算法及模板详解

⭐写在前面的话：本系列文章旨在复习算法刷题中常用的基础算法与数据结构，配以详细的图例解释，总结相应的代码模板，同时结合例题以达到最佳的学习效果。本专栏面向算法零基础但有一定的C++基础的学习者。若C++基础不牢固，可参考：10min快速回顾C++语法，进行语法复习。

文章目录

• 差分
• • 一维差分
  • • 例题：差分
    • • 代码模板
      • 二维差分
      • • 例题：差分矩阵
        • • 代码模板

            差分

            一维差分

            差分思想和前缀和是相反的。

            首先我们先定义数组a, 其中a[1],a[2]…a[n]作为前缀和。

            然后构造数组b，b[1],b[2]…b[n]为差分数组。其中通过差分数组的前缀和来表示a数组，即a[n] = b[1] + b[2]+…+b[n]。

            一维差分数组的构造也很简单，即a[1] = b[1], b[2] = a[2] - a[1], b[n] = a[n] - a[n-1]；

            注意：刚开始时可以初始化数组a,b全部为0，输入a数组后；在构造时，只需要将b[1]看做在[1, 1]区间上加上a[1]; b[2] 看作在[2, 2]区间上加上a[2]；

            //eg:对于b[1]:
            b[1] = 0 + a[1];
            b[2] = 0 - a[1]; 	//最终：b[1] = a[1]
            //对于b[2]:
            b[2] = b[2] + a[2];  //==> 最终：b[2] = a[2] - a[1]
            b[3] = b[3] - a[2];
            

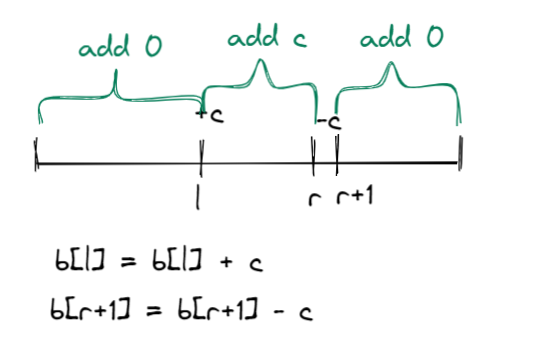
            差分数组的好处是可以简化运算，例如想要给一个区间 [l,r] 上的数组加一个常数c，原始的方法是依次加上c，这样的时间复杂度是O(n)的。但是如果采用差分数组的话，可以大大降低时间复杂度到O(1)。

            由于a[n] = b[1] + b[2]+…+b[n]，因此只需要将b[l] = b[l] + c 即可，这样l之后的数字会依次加上常数c，而在 b[r]处，将b[r+1] = b[r+1] - c ，这样r之后的数组又会恢复原值，仅需要处理这两个边界的差分数组即可，时间复杂度大大降低。

            

            例题：差分

            输入一个长度为 n 的整数序列。

            接下来输入 m 个操作，每个操作包含三个整数 l,r,c，表示将序列中 [l,r] 之间的每个数加上 c。

            请你输出进行完所有操作后的序列。

            输入格式

            第一行包含两个整数 n 和 m。

            第二行包含 n 个整数，表示整数序列。

            接下来 m 行，每行包含三个整数 l，r，c表示一个操作。

            输出格式

            共一行，包含 n 个整数，表示最终序列。

            数据范围

            1≤n,m≤100000,

            1≤l≤r≤n,

            −1000≤c≤1000,

            −1000≤整数序列中元素的值≤1000

            输入样例：

            6 3
            1 2 2 1 2 1
            1 3 1
            3 5 1
            1 6 1
            

            输出样例：

            3 4 5 3 4 2
            

            代码模板

            #include
            using namespace std;
            const int N = 100010;
            int m,n;
            int a[N],b[N];
            void insert(int l, int r , int c)
            {
                b[l] += c;
                b[r+1] -= c;
            }
            int main()
            {
                scanf("%d%d",&n, &m);
                for(int i = 1; i 
                    int l, r ,c;
                    scanf("%d%d%d",&l, &r, &c);
                    insert(l, r, c);
                    
                }
                for(int i = 1; i 
                b[x1][y1] += c;
                b[x2 + 1][y1] -= c;
                b[x1][y2 +1] -= c;
                b[x2 +1][y2+1] +=c;
            }
            int main()
            {
                scanf("%d%d%d", &n, &m, &q);
                
                for(int i = 1; i 
                    int x1, x2, y1, y2, c;
                    cin  x1  y1 x2  y2 >> c;
                    insert(x1,y1, x2, y2, c);
                }
                
                //求前缀和
                
                for(int i = 1; i
                    for(int j = 1; j