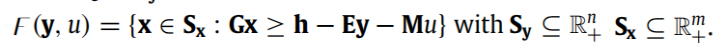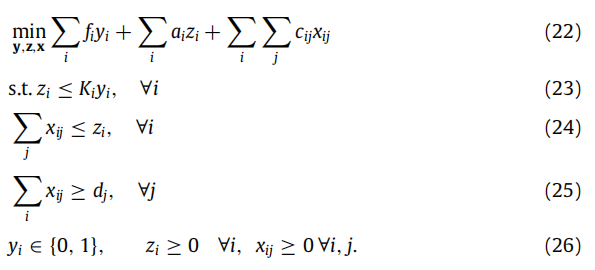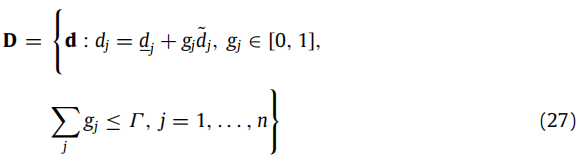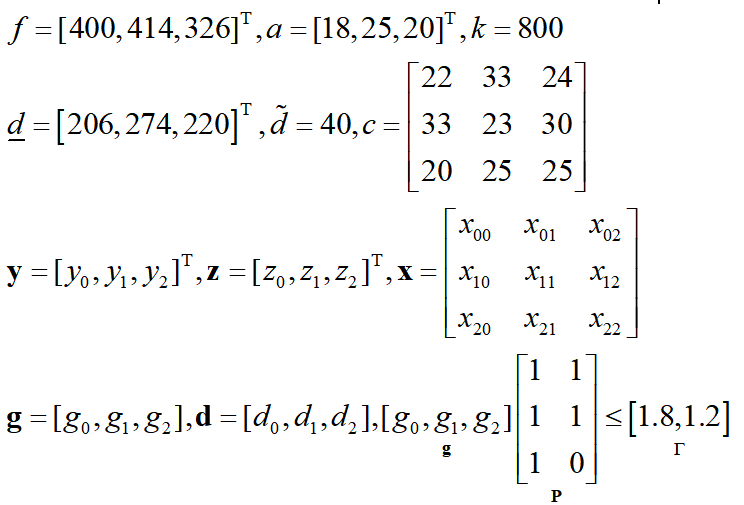鲁棒优化入门(4)-两阶段鲁棒优化及行列生成算法(C&CG)超详细讲解(附matlab代码)
本文的主要参考文献:
Zeng B , Zhao L . Solving Two-stage Robust Optimization Problems by A Constraint-and-Column Generation Method[J]. Operations Research Letters, 2013, 41(5):457-461.
1.两阶段鲁棒优化问题的引入
鲁棒优化是应对数据不确定性的一种优化方法,但单阶段鲁棒优化过于保守。为了解决这一问题,引入了两阶段鲁棒优化(Two-stage Robust Optimization)以及更一般的多阶段鲁棒优化,其核心思想是将决策问题分为两个阶段。第一阶段是进行初步决策,第二阶段是根据第一阶段的决策结果制定更好的决策策略,应对数据不确定性的影响。这种方法可以降低保守性,提高鲁棒性。
假设一阶段和二阶段决策问题都是线性规划,并且不确定性集合U是一个有限的离散集合或者多面体集。使用y表示第一阶段决策变量,x表示第二阶段决策变量,表示不确定矢量。在此假设下的两阶段鲁棒优化的一般形式为:
其中:
向量c,b,d,h和矩阵A , G , E , M都是确定性的数值,不确定性体现在向量u上。注意到第二阶段优化的约束条件F(y,u)是关于不确定性u的线性函数。
原文献中提供了以运输问题作为算例,具体如下:
其中,yi为0-1变量,表示是否在i地建设仓库,zi表示仓库i储存的商品数量,xij表示从i仓库到j客户运送的商品数量,fi表示建设仓库i的固定成本,ai表示仓库i存储商品的单位成本,cij表示从i仓库到j客户运送单位商品的成本,ki表示仓库i的最大容量,dj表示客户j的需求。
不确定变量为客户的需求,表达方式如下:
具体算例参数:
根据上面的公式,我们可以写出各个参数矩阵以及变量的表达式:
用matlab代码表示:
%% 参数矩阵 f = [400; 414; 326]; a = [18; 25; 20]; k = 800; C = [22, 33, 24; 33, 23, 30; 20, 25, 27]; d_ = [206; 274; 220]; d_wave = 40; gamma = [1.8,1.2]; P = [1 1;1 1;1 0]; %% 决策变量 y = binvar(3,1); z = sdpvar(3,1); x = sdpvar(3,3,’full’); d = sdpvar(3,1); g = sdpvar(3,1);
可以尝试求解一下这个确定性优化问题,和后面的两阶段鲁棒优化进行对比:
%% 目标函数 objective = f'*y + a'*z + sum(sum(C.*x)); %% 约束条件 Constraints = []; Constraints = [Constraints , z >= 0 , x >= 0 , g >= 0 , g