【Unity面试篇】Unity 面试题总结甄选｜算法相关 | ❤️持续更新❤️

03-01 1430阅读

前言

之前整理了一篇关于Unity面试题相关的所有知识点：2022年Unity 面试题 |五萬字二佰道| Unity面试题大全，面试题总结【全网最全，收藏一篇足够面试】
为了方便大家可以重点复习某个模块，所以将各方面的知识点进行了拆分并更新整理了新的内容，并对之前的版本中有些模糊的地方进行了纠正。
进阶篇中有些题目在基础篇已经有了，这里划分模块时有些会再加一遍用于加深印象学习。
所以本篇文章就来整理一下算法相关的题目，说不准就会面试的时候就会遇到！
【Unity面试篇】Unity 面试题总结甄选｜算法相关 | ❤️持续更新❤️
- - - 前言
    - 💞算法
    - - 1.十大排序简述
        2. 请写一个方法判断一个整数是奇数还是偶数。
        3. 请写一个方法判断一个整数是否是2的n次方。
        4. 对字节变量，其二进制表示法中求有多少个1，如 00101010则返回值为 3，也是要求效率最高。
        5. 100万的数据选出前1万大的数
        6. 二分查找
        7. BFS（广度优先搜索）
        8.DFS（深度优先搜索）
        9. 请写出求斐波那契数列任意一位的值的算法
        10. 下列代码在运行中会产生几个临时对象？
        11. 怎么判断一个点是否在直线上
        12. 判断点是否在线段上
        👥总结
        
        
        💞算法
        
        想锻炼算法相关内容注意推荐去刷题网站勤加练习，如力扣、牛客网等。
        
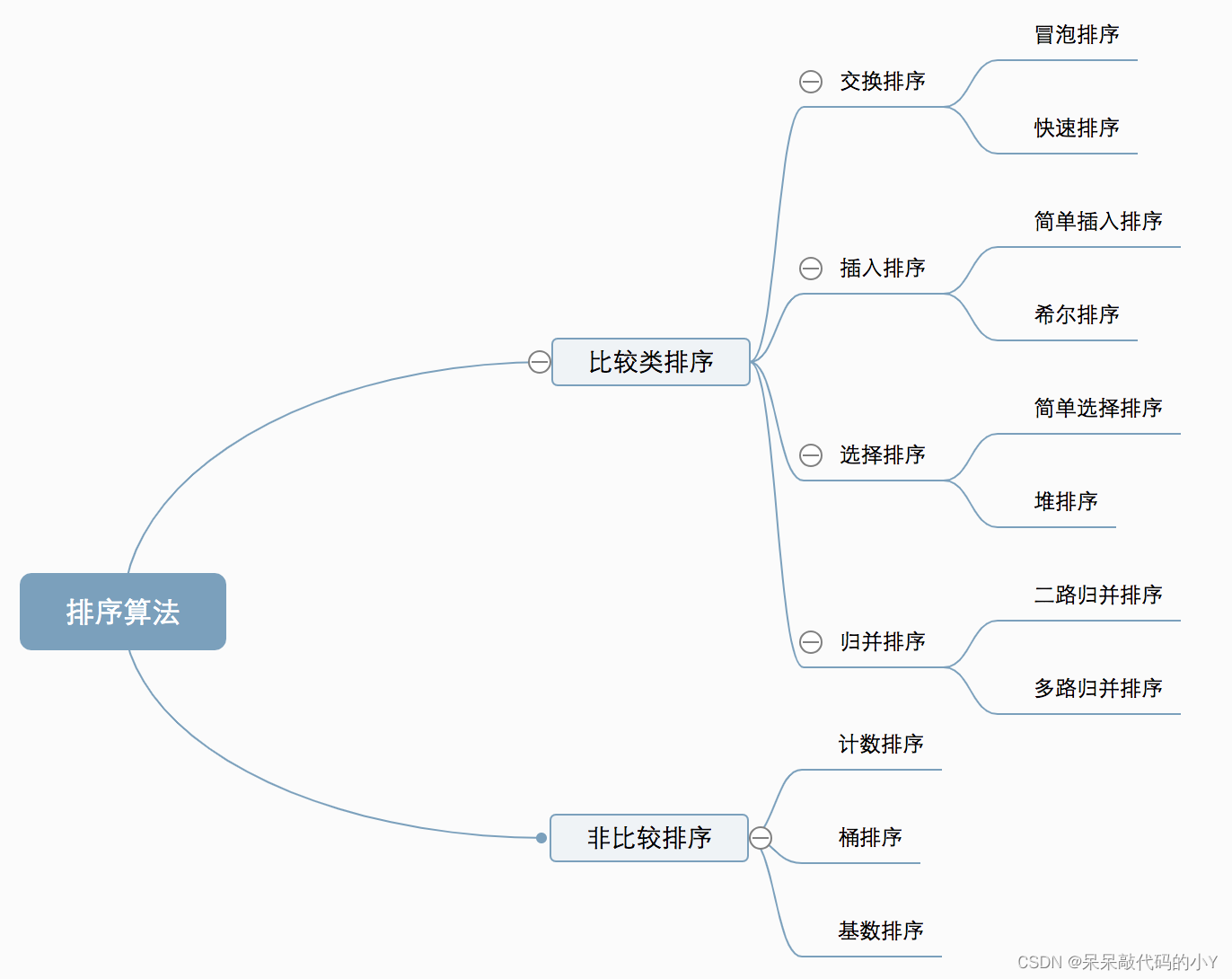
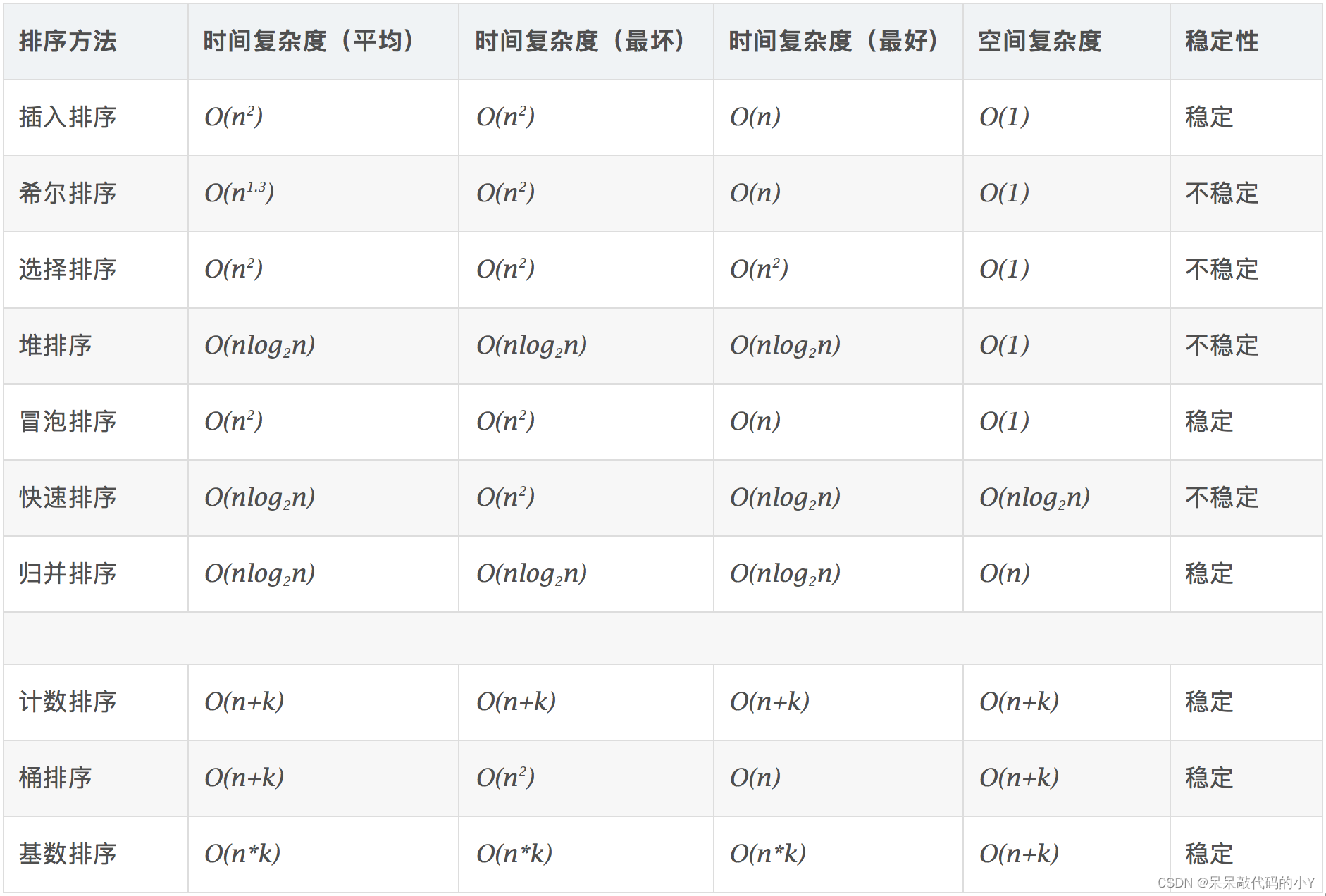
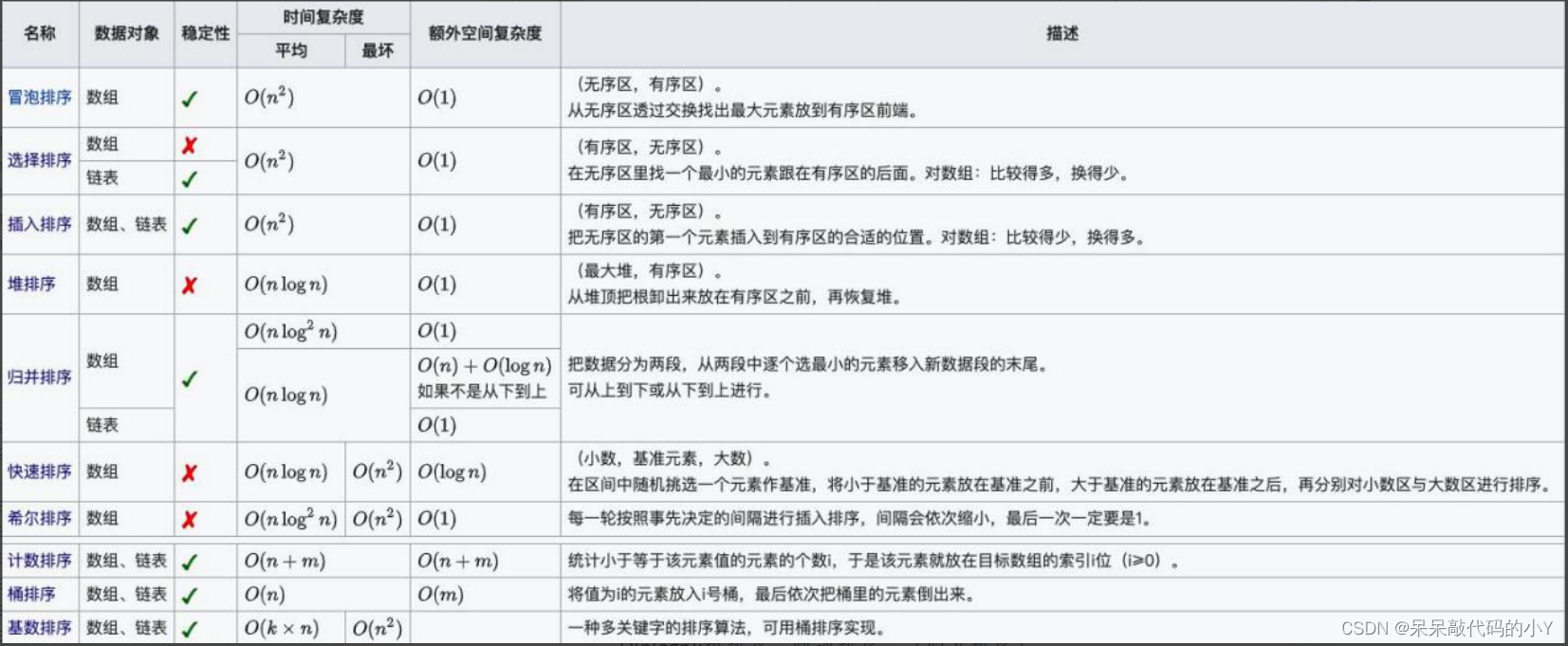
        1.十大排序简述
        
        十种常见排序算法可以分为两大类：
        
        比较类排序：通过比较来决定元素间的相对次序，由于其时间复杂度不能突破O(nlogn)，因此也称为非线性时间比较类排序。
        非比较类排序：不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此也称为线性时间非比较类排序。
        冒泡排序（Bubble Sort）
        冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
        选择排序（Selection Sort）
        选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。
        插入排序（Insertion Sort）
        插入排序（Insertion-Sort）的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。
        希尔排序（Shell Sort）
        1959年Shell发明，第一个突破O(n2)的排序算法，是简单插入排序的改进版。它与插入排序的不同之处在于，它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。
        归并排序（Merge Sort）
        归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为2-路归并。
        快速排序（Quick Sort）
        快速排序的基本思想：通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录继续进行排序，以达到整个序列有序。
        堆排序（Heap Sort）
        堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。
        计数排序（Counting Sort）
        计数排序不是基于比较的排序算法，其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。
        桶排序（Bucket Sort）
        桶排序是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。桶排序 (Bucket sort)的工作的原理：假设输入数据服从均匀分布，将数据分到有限数量的桶里，每个桶再分别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排）。
        基数排序（Radix Sort）
        基数排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序。最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前。
        2. 请写一个方法判断一个整数是奇数还是偶数。
        
        常规答案
        与2取余，若为0则是偶数，否则为奇数。
        
        public static bool IsEven(int number) { return ((number % 2) == 0); }
        
        进阶答案
        检测数字的二进制最低位是否为0。将最低位和1相与，如果结果为0，则为偶数，否则为奇数。
        
        如奇数3和1位与，实际上是 00000000 00000000 00000000 00000011 & 00000000 00000000 00000000 00000001 --------------------------------------------- 00000000 00000000 00000000 00000001
        
        再比如偶数6和1位与，实际上是 00000000 00000000 00000000 00000110 & 00000000 00000000 00000000 00000001 --------------------------------------------- 00000000 00000000 00000000 00000000
        
        判断一个整数是奇数还是偶数 /** /// 判断一个整数是否是偶数 /// /// 传入的整数 /// 如果是偶数，返回true，否则为false public static bool IsEven(int number) { return ((number & 1) == 0); } /** /// 判断一个整数是否是奇数 /// /// 传入的整数 /// 如果是奇数，返回true，否则为false public static bool IsOdd(int number) { return !IsEven(number); }
        
        3. 请写一个方法判断一个整数是否是2的n次方。
        
        常规答案
        利用位运算进行判断，将一个数通过不断位右移，最终结果若为1则为true，否则为false。
        
        判断一个整数是否是2的n次方 public static bool IsPower(int number) { if (number return false; } while (true) { if (number == 1) { return true; } //如果是奇数 if ((number & 1) == 1) { return false; } //右移一位 number >= 1; } }
        
        进阶答案
        2的n次方其二进制表示只有1个1，如整数8，其二进制表示形式是00001000，减去1后为00000111，让这两者进行位与的结果刚好是0则为true，否则就是falsez。
        
        判断一个整数是否是2的n次方 public static bool IsPower(int number) { if (number return false; } if ((number & (number - 1)) == 0) { return true; } return false; } int count = 0; if (data == 0) { } else if (data 0) { while (data > 0) { data &= (data - 1); count++; } } else { int minValue = -0x40000001; while (data > minValue) { data &= (data - 1); count++; } count++; } return count; }
        
        5. 100万的数据选出前1万大的数
        
        利用堆排序、小顶堆实现。
        
        先拿10000个数建堆，然后一次添加剩余元素，如果大于堆顶的数（10000中最小的），将这个数替换堆顶，并调整结构使之仍然是一个最小堆，这样遍历完后，堆中的10000个数就是所需的最大的10000个。建堆时间复杂度是O（mlogm），算法的时间复杂度为O (nmlogm)（n为100，m为10000）。
        
        优化的方法：分治。可以把所有10亿个数据分组存放，比如分别放在1000个文件中。这样处理就可以分别在每个文件的10^6个数据中找出最大的10000个数，合并到一起在再找出1000*10000中的最终的结果。
        
        6. 二分查找
        
        算法思路：假设目标值在闭区间[l, r]中，每次将区间长度缩小一半，当l = r时，我们就找到了目标值。
        
        1.当我们将区间[l, r]划分成[l, mid]和[mid + 1, r]时，其更新操作是r = mid或者l = mid + 1;，计算mid时不需要加1。(常用)
        
        int bsearch_1(int 1, int r) { While (l int mid = l +r > 1; if(check(mid)) r = mid; else l = mid + 1; } return l; }
        
        2.当我们将区间[l, r]划分成[l, mid - 1]和[mid, r]时，其更新操作是r = mid - 1或者l = mid;，此时为了防止死循环，计算mid时需要加1。
        
        int bsearch_2(int 1, int r) { While (l int mid = l + r +1 > 1; if(check(mid)) l = mid; else r = mid - 1; } return l; }
        
        3.代码里的if语句，若变成一个bool函数带入对应的l，r，mid，array等，在函数里面继续二分查找，即可变成“二分答案”。
        
        7. BFS（广度优先搜索）
        
        BFS从根节点开始搜索，并根据树级别模式探索所有邻居根。它使用队列数据结构来记住下一个节点访问。
        
        1.如果不需要确定当前遍历到了哪一层
        
        while queue 不空: cur = queue.pop() for 节点 in cur的所有相邻节点: if 该节点有效且未访问过: queue.push(该节点)
        
        2.如果要确定当前遍历到了哪一层，BFS 模板如下。这里增加了 level 表示当前遍历到二叉树中的哪一层了，也可以理解为在一个图中，现在已经走了多少步了。size 表示在当前遍历层有多少个元素，也就是队列中的元素数，我们把这些元素一次性遍历完，即把当前层的所有元素都向外走了一步。
        
        level = 0 while queue 不空: size = queue.size() while (size --) { cur = queue.pop() for 节点 in cur的所有相邻节点: if 该节点有效且未访问过: queue.push(该节点) } level++;
        
        8.DFS（深度优先搜索）
        
        注意搜索的顺序；当搜到叶子节点（递归结束）时就回溯，回退一步看一步。
        
        DFS从根节点开始搜索，并从根节点尽可能远地探索这些节点。使用堆栈数据结构来记住下一个节点访问。
        
        类似于树的先序遍历
        
        
        
        9. 请写出求斐波那契数列任意一位的值的算法
        
        static int Fn(int n) { if (n throw new ArgumentOutOfRangeException(); } if (n == 1||n==2) { return 1; } return checked(Fn(n - 1) + Fn(n - 2)); // when n46 memory will overflow }
        
        10. 下列代码在运行中会产生几个临时对象？
        
        string a = new string("abc"); a = (a.ToUpper() +"123").Substring(0,2);
        
        实在C#中第⼀⾏是会出错的（Java中倒是可⾏）。
        应该这样初始化：
        
        string b = new string(new char[] {'a','b','c'});
        
        三个临时对象：abc、ABC、AB
        
        11. 怎么判断一个点是否在直线上
        
        已知点P(x,y)，以及直线上的两点A(x1,y1)、B(x2,y2)，可以通过计算向量AP与向量AB的叉乘是否等于0来计算点P是否在直线AB上。
        
        知识点：叉乘
        
        /// /// 2D叉乘 /// /// 点1 /// 点2 /// public static float CrossProduct2D(Vector2 v1,Vector2 v2) { //叉乘运算公式 x1*y2 - x2*y1 return v1.x * v2.y - v2.x * v1.y; } /// /// 点是否在直线上 /// /// /// /// /// public static bool IsPointOnLine(Vector2 point, Vector2 lineStart, Vector2 lineEnd) { float value = CrossProduct2D(point - lineStart, lineEnd - lineStart); return Mathf.Abs(value) //叉乘运算公式 x1*y2 - x2*y1 return v1.x * v2.y - v2.x * v1.y; } /// float value = CrossProduct2D(point - lineStart, lineEnd - lineStart); return Mathf.Abs(value) //1.先通过向量的叉乘确定点是否在直线上 //2.在拍段点是否在指定线段的矩形范围内 if (IsPointOnLine(point,lineStart,lineEnd)) { //点的x值大于最小，小于最大x值以及y值大于最小，小于最大 if (point.x = Mathf.Min(lineStart.x, lineEnd.x) && point.x