【算法小课堂】二分查找算法

简单思路：

当我们要从一个序列中查找一个元素的时候，最快想到的方法就是顺序查找法（即：从前到后依次查找）。但这种方法过于无脑，就是暴力的把每个元素都排查一遍。元素个数少的时候还行，一旦元素个数多起来，效率是非常低下，所以在实际中这种查找的方法是被摒弃的。

当题目或者实际对时间复杂度有着很高的要求的时候，这种暴力解法就显得很乏力

这里就不得不介绍一种简单且效率较高的查找方法了：二分查找法，又称折半查找法。但该方法是建立在有序的前提下的，基本思路就是：

利用两个指针left和right，不断取中点来不断把区间减小从而找到我们的答案

二分查找法的优势：

• 二分查找法的时间复杂度：O（logN）

• 暴力解法的时间复杂度：O（N）

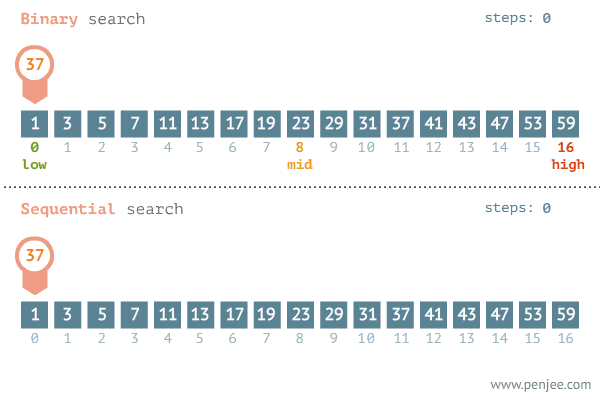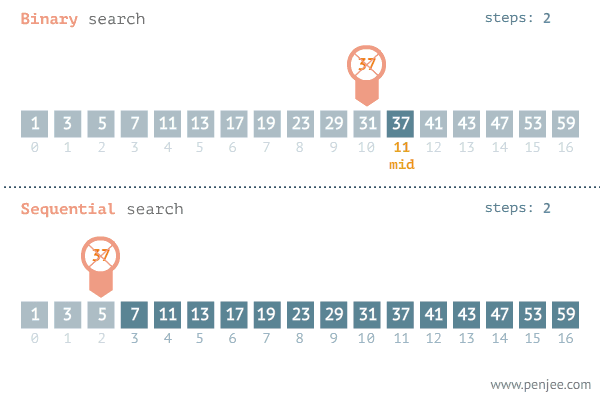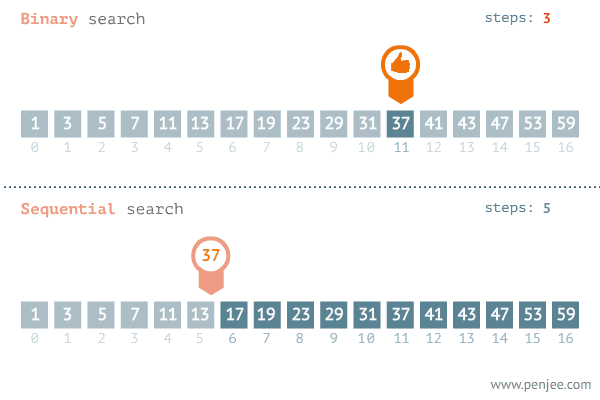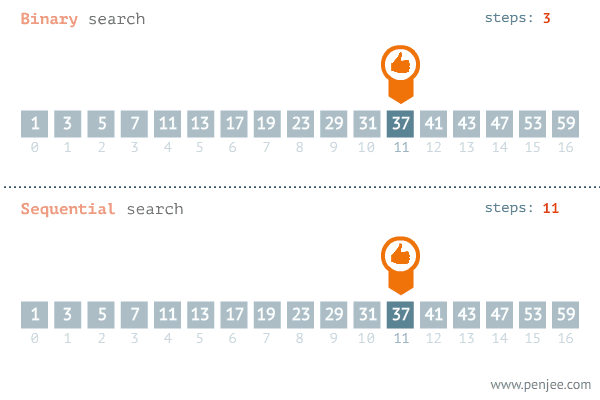
  如何直观来体现二分查找法时间复杂度的优势呢？

  

  可以看出 二分查找 在查找数字 37 时只需3次，而 顺序查找 在查找37时需要12次。

  二分查找的条件：

  很多算法书都是写的具有有序性，其实更准确的是具有二段性

  • 也就是具有可以把数组分为两端的性质

    二分查找有两个限制条件：

    1. 查找的数量只能是一个，不能是多个
    2. 查找的对象在逻辑上必须是有序的（这个不是必要条件，更深层次是就有二段性）

    朴素二分查找：

    1.left=0，right=数组最后一个位置的下标

    2.取中点：mid=（right-left）/2

    二分法的思想很简单，因为整个数组是有序的，数组默认是递增的。

    首先选择数组中间的数字和需要查找的目标值比较

    • 如果相等最好，就可以直接返回答案了

    • 如果不相等

      如果中间的数字大于目标值，则中间数字向右的所有数字都大于目标值，全部排除

      如果中间的数字小于目标值，则中间数字向左的所有数字都小于目标值，全部排除

      704. 二分查找

      以此题为例：

      class Solution {
      public:
          int search(vector& nums, int target) {
              int left=0;
              int right=nums.size()-1;
              while(left
                  int mid=left+(right-left)/2;
                  if(nums[mid]==target) return mid;
                  if(nums[mid]target) right=mid-1;
                  if(nums[mid]
                  int mid=left+(right-left)/2;
                  if(nums[mid]==target) return mid;
                  if(nums[mid]target) ...;
                  if(nums[mid]
      public:
          vector
              //特殊情况处理一下
              if(nums.size()==0)return {-1,-1};
              int left=0,right=nums.size()-1;
              vector
                  int mid=left+(right-left)/2;
                  if(nums[mid]-1,-1};
              else ret.push_back(left);
              //查找右端点
              left=0,right=nums.size()-1;
              while(left
                  int mid=left+(right-left+1)/2;
                  if(nums[mid]-1,-1};
              else ret.push_back(right);
              return ret;
          }
      };