偏最小二乘(PLS)原理分析&Python实现
目录
1 偏最小二乘的意义
2 PLS实现步骤
3 弄懂PLS要回答的问题
4 PLS的原理分析
4.1 自变量和因变量的主成分求解原理
4.1.1 确定目标函数
4.1.2 投影轴w1和v1的求解
4.2 求解回归系数
5 第3章问题解答
5.1 PCA原理
5.2 为什么要对X、Y标准化？
5.3 如何求自变量和因变量的第一主成分
5.4 为什么要计算残差矩阵？为什么要不停地用残差矩阵替换原来的自变量和因变量；
5.5 为什么要进行交叉性检验？
6 PLS代码实现——Python
1 偏最小二乘的意义
回归是研究因变量对自变量的依赖关系的一种统计分析方法，目的是通过自变量的给定值来估计或预测因变量的值。
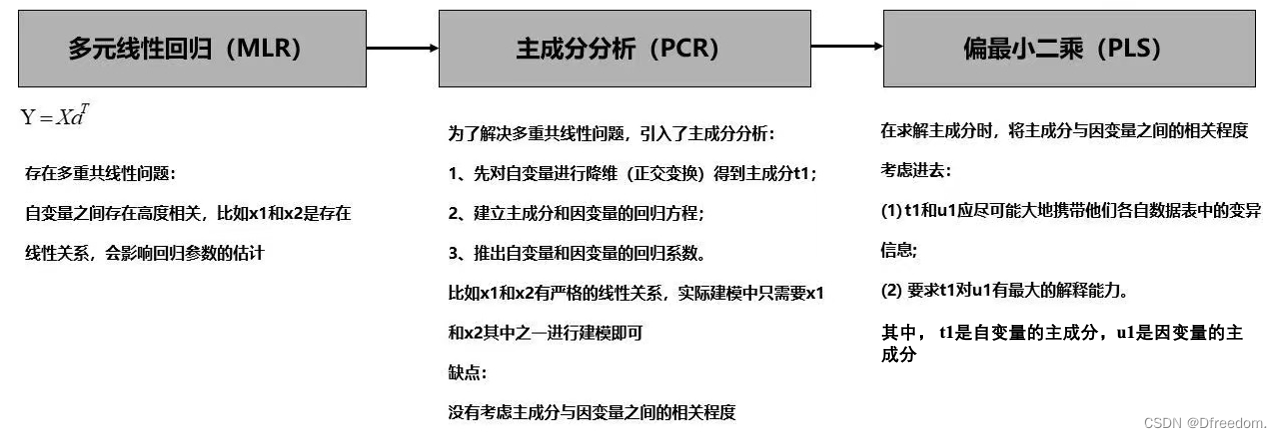
当自变量只有一个时，常用的回归方法有一元线性回归（SLR）；当自变量有多个时，常用的回归方法有多元线性回归（MLR）、主成分回归（PCR）、偏最小二乘回归（PLS）等，这几种回归方法的联系和区别如下：
从中可以看出，偏最小二乘是主成分分析+线性回归的合体，集合了两者的优点。一般来说，能用主成分分析，就一定能用偏最小二乘。当数据量小，甚至比变量维数还小，而相关性又比较大时使用，偏最小二乘是优于主成分回归。
2 PLS实现步骤
设自变量矩阵是X，因变量矩阵是Y：
① 标准化自变量矩阵和因变量矩阵，标准化后的矩阵是E和F；
② 求解自变量和因变量的第一主成分t1、u1；
③ 建立自变量E、因变量E和第一主成分t1、u1的回归方差，并计算残差矩阵E1、F1；
④ 用E1、F1代替E、F形成新的自变量、因变量，求解新的自变量和因变量的第一主成分t2、u2，即为原来自变量和因变量的第二主成分。
⑤ 建立新的自变量E1、因变量F1（残差矩阵）和第二主成分t2、u2的回归方程，并计算残差矩阵E2，F2；
⑥ 重复④、⑤步直至求出所有的主成分或者满足条件为止；
⑦ 交叉性检验，确定满足条件的主成分个数；
⑧ 建立回归方程，计算出回归系数。
3 弄懂PLS要回答的问题
① PCA的原理；
② 为什么要对X、Y标准化；
③ 如何求自变量和因变量的第一主成分；
④ 为什么要计算残差矩阵？为什么要不停地用残差矩阵替换原来的自变量和因变量；
⑤ 为什么要进行交叉性检验？
4 PLS的原理分析
从PLS的求解步骤可以看出，有两个关键点：
① 求解自变量和因变量的主成分；
② 求解回归系数。
4.1 自变量和因变量的主成分求解原理
设有p个自变量，q个以因变量，样本点个数为n，则可以得到自变量和因变量的数据表:
其中，和
是n维列向量。
偏最小二乘的思想是求解主成分的同时要保证自变量和因变量的相关性最大。即求解X的主成分t1和Y的主成分u1，t1和u1需要满足如下要求：
(1) t1和u1应尽可能大地携带他们各自数据表中的变异信息；
(2) t1与u1的相关程度能够达到最大。
从上述原理可以看出，PLS和PCA求解主成分都是一个目标函数最大值求解的问题。区别在于两者的目标函数不一样。所以同样地，PLS求解主成分有关键的两个步骤：
1、确定目标函数；
2、求解目标函数取最大值时的投影轴w1和v1。
4.1.1 确定目标函数
① 要使主成分t1尽可能携带X的信息或者u1尽可能携带Y的信息，则有：
② 要使主成分t1和u1之间的相关程度最高，则有：
要同时满足以上两个要求，则目标函数可表示成：
因为t1、u1分别是X、Y投影得到，设t投影轴为w1、v1，则有：
又w1、v1为方向向量，且E、F已经标准化，列向量的均值为0，则目标函数可转换为：
其中，
4.1.2 投影轴w1和v1的求解
投影轴w1和 v1求解的问题，可以描述为：
已知自变量和因变量标准化后的数据表E和F，求投影轴w1、v1使得：
其中，
这是一个条件极值的问题，可以采用拉格朗日乘子法求解，构造拉格朗日函数：
对v，w求偏导数：
两边同时乘以、
,则有：
所以有：，将
带入上述方程可得：
是矩阵
最大特征值值对应的特征向量，求出
就可求出
。
至此就可以求解出自变量和因变量的第一主成分:
4.2 求解回归系数
建立E、F和t1、u1之间的回归方程:
式中，m1、k1、n1回归系数，E1、F1*、F1为残差矩阵。回归系数计算公式为：
采用残差矩阵E1、F1代替E、F继续求解，即为第二主成分t2、u2。直到求出所有主成分或者满足要求（后面说明）。
设E的秩为A，则有：
由于t1、t2、......、tA都可以表示成的线性组合，所以可得：
其中，为残差矩阵的第
列。
为第
列因变量对应的回归系数。
本章小结：
设自变量X=，Y=
,
为列向量。X、Y标准化以后的矩阵为E、F。
1、第一主成分的投影轴是矩阵最大特征值对应的特征向量；
2、求解残差矩阵E1、F1，第二成分是矩阵最大特征值对应的特征向量；
3、以此类推，可以求出第三、四.........主成分。
4、用因变量是主成分的线性组合，主成分是自变量的线性组合，以此可得出回归系数。
5 第3章问题解答
5.1 PCA原理
要学习PLS，弄懂PCA的原理是前提条件：
主成分分析(PCA)原理分析&Python实现_Dfreedom.的博客-CSDN博客
5.2 为什么要对X、Y标准化？
当行数等于样本数，列数等于特征数时，标准化是按列进行的，分为两步：
① 每一列先减去每一列的均值；
② 每一列再除以每一列标准差。
可以看出和PCA的处理有点差别，PCA只进行了第一步（去均值）。PLS的去均值和PCA的去均值理由是一样的：目标函数的化简是基于每一列的均值为0求出的：
求解目标函数的这个等式成立的前提是E和F去均值。
那为什么还要除以标准差呢？为什么PCA不是必须要除以标准差呢？
① PLS求解时需要考虑自变量和因变量的相关性，协方差作为描述X和Y相关程度的量，在同一物理量纲之下有一定的作用，但同样的两个量采用不同的量纲使它们的协方差在数值上表现出很大的差异。所以需要将除以标准差将自变量和因变量统一在同一个量纲里；
② PCA在求解时不需要考虑相关性，所以只是中心化就足够。当然也可以标准化。
即：PCA可以只中心化，也可以继续标准化，PLS就必须标准化，不能只是中心化。
5.3 如何求自变量和因变量的第一主成分
设自变量和因变量标准化后的矩阵是E和F，从4.1章节的推导过程可知，自变量的第一主成分的投影轴w1是矩阵最大特征值值对应的特征向量，求出w1可根据公式
求出因变量第一主成分的投影轴v1。知道投影轴以后就可以根据投影的计算公式得到第一主成分：
5.4 为什么要计算残差矩阵？为什么要不停地用残差矩阵替换原来的自变量和因变量；
如果只是根据目标函数求解出自变量和因变量的主成分，会出现与CCA一样的不能由X到Y映射的问题。可以从误差的角度来理解，在回归分析中，得到回归系数以后，用自变量去估计因变量会存在误差，称之为残差，如下公式：
式中，为第一主成分和回归系数的乘积，E为残差矩阵。为了减小估计误差也就是残差，继续求解残差的第一主成分，将残差用表示成自变量的线性组合，从而就可以减小回归误差：
式中，Ek是残差，k是选择的主成分个数。显而易见k越大，残差就越小，所以一般情况下，只要迭代足够多的次数，就可以将回归误差减小到满足目标要求。M1称为第一主成分，M2称为第二主成分，以此类推。
5.5 为什么要进行交叉性检验？
原因：在许多情形下,偏最小二乘回归方程并不需要选用全部的成分进行回归建模,而是可以象在主成分分析一样,采用截尾的方式选择前m 个成分,仅用这m 个后续的成分就可以得到一个预测性较好的模型。事实上,如果后续的成分已经不能为解释因变量提供更有意义的信息时,采用过多的成分只会破坏对统计趋势的认识,引导错误的预测结论。
交叉性检验的判定条件是预测平方误差和与误差平方和的比值，本文不作详细的介绍，有兴趣的可以阅读文章末尾的参考链接。
6 PLS代码实现——Python
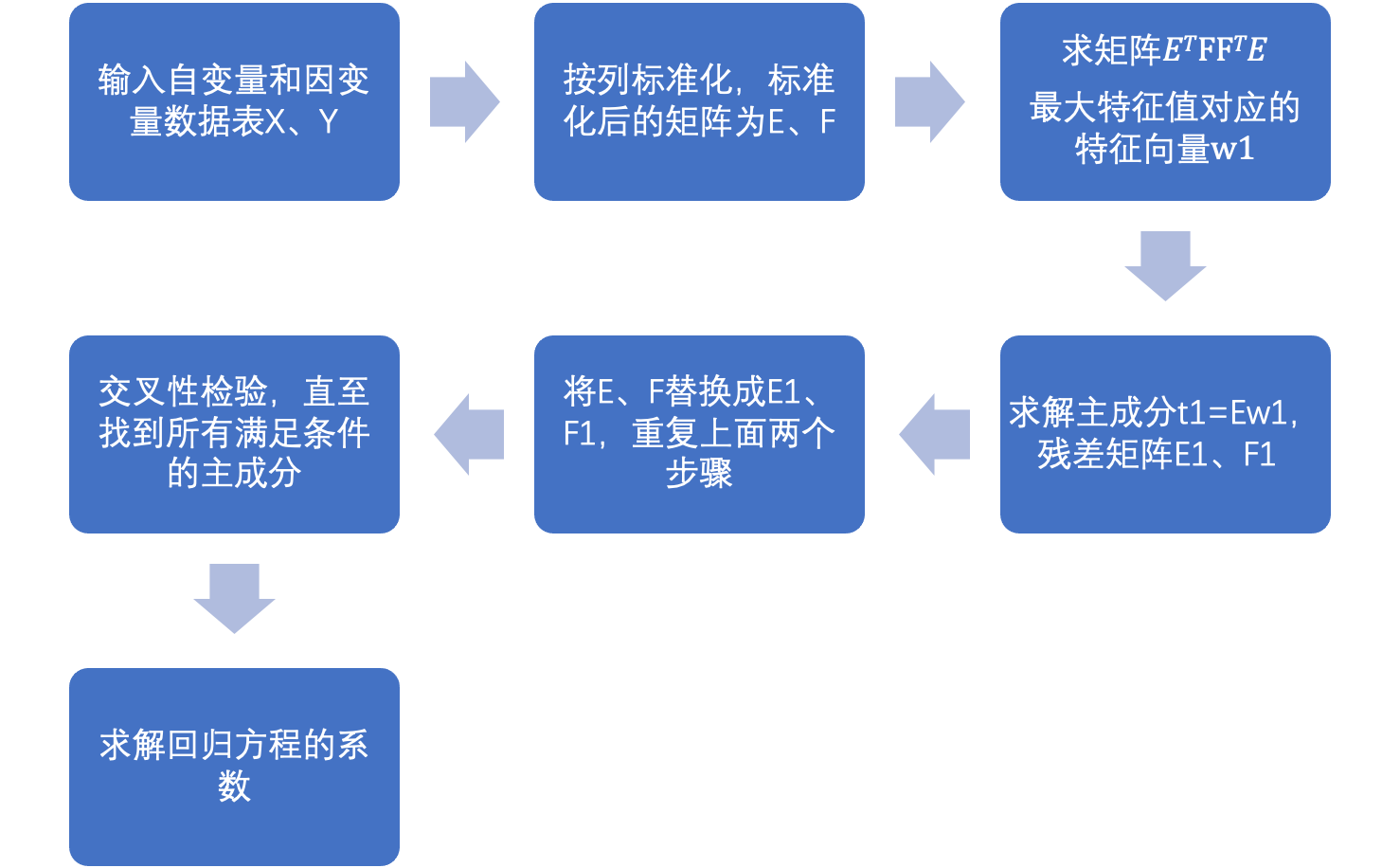
程序流程图：
Python代码：
import numpy as np
x1=[191,189,193,162,189,182,211,167,176,154,169,166,154,247,193,202,176,157,156,138]
x2=[36,37,38,35,35,36,38,34,31,33,34,33,34,46,36,37,37,32,33,33]
x3=[50,52,58,62,46,56,56,60,74,56,50,52,64,50,46,62,54,52,54,68]
y1=[5,2,12,12,13,4,8,6,15,17,17,13,14,1,6,12,4,11,15,2]
y2=[162,110,101,105,155,101,101,125,200,251,120,210,215,50,70,210,60,230,225,110]
y3=[60,60,101,37,58,42,38,40,40,250,38,115,105,50,31,120,25,80,73,43]
#-----数据读取
data_raw=np.array([x1,x2,x3,y1,y2,y3])
data_raw=data_raw.T #输入原始数据，行数为样本数，列数为特征数
#-----数据标准化
num=np.size(data_raw,0) #样本个数
mu=np.mean(data_raw,axis=0) #按列求均值
sig=(np.std(data_raw,axis=0)) #按列求标准差
data=(data_raw-mu)/sig #标准化，按列减去均值除以标准差
#-----提取自变量和因变量数据
n=3 #自变量个数
m=3 #因变量个数
x0=data_raw[:,0:n] #原始的自变量数据
y0=data_raw[:,n:n+m] #原始的变量数据
e0=data[:,0:n] #标准化后的自变量数据
f0=data[:,n:n+m] #标准化后的因变量数据
#-----相关矩阵初始化
chg=np.eye(n) #w到w*变换矩阵的初始化
w=np.empty((n,0)) #初始化投影轴矩阵
w_star=np.empty((n, 0)) #w*矩阵初始化
t=np.empty((num, 0)) #得分矩阵初始化
ss=np.empty(0) #或者ss=[]，误差平方和初始化
press=[] #预测误差平方和初始化
Q_h2=np.zeros(n) #有效性判断条件值初始化
#-----求解主成分
for i in range(n): #主成分的总个数小于等于自变量个数
#-----求解自变量的最大投影w和第一主成分t
matrix=e0.T@f0@f0.T@e0 #构造矩阵E'FF'E
val,vec=np.linalg.eig(matrix) #计算特征值和特征向量
index=np.argsort(val)[::-1] #获取特征值从大到小排序前的索引
val_sort=val[index] #特征值由大到小排序
vec_sort=vec[:,index] #特征向量按照特征值的顺序排列
w=np.append(w,vec_sort[:,0][:,np.newaxis],axis=1) #储存最大特征向量
w_star=np.append(w_star,chg@w[:,i][:,np.newaxis],axis=1) #计算 w*的取值
t=np.append(t,e0@w[:,i][:,np.newaxis],axis=1) #计算投影
alpha=e0.T@t[:,i][:,np.newaxis]/(t[:,i]@t[:,i]) #计算自变量和主成分之间的回归系数
chg=chg@(np.eye(n)-(w[:,i][:,np.newaxis]@alpha.T)) #计算 w 到 w*的变换矩阵
e1=e0-t[:,i][:,np.newaxis]@alpha.T #计算残差矩阵
e0=e1 #更新残差矩阵
#-----求解误差平方和ss
beta=np.linalg.pinv(t)@f0 #求回归方程的系数，数据标准化，没有常数项
res=np.array(f0-t@beta) #求残差
ss=np.append(ss,np.sum(res**2))#残差平方和
#-----求解残差平方和press
press_i=[] #初始化误差平方和矩阵
for j in range(num):
t_inter=t[:,0:i+1]
f_inter=f0
t_inter_del=t_inter[j,:] #把舍去的第 j 个样本点保存起来,自变量
f_inter_del=f_inter[j,:] #把舍去的第 j 个样本点保存起来，因变量
t_inter= np.delete(t_inter,j,axis=0) #删除自变量第 j 个观测值
f_inter= np.delete(f_inter,j,axis=0) #删除因变量第 j 个观测值
t_inter=np.append(t_inter,np.ones((num-1,1)),axis=1)
beta1=np.linalg.pinv(t_inter)@f_inter # 求回归分析的系数,这里带有常数项
res=f_inter_del-t_inter_del[:,np.newaxis].T@beta1[0:len(beta1)-1,:]-beta1[len(beta1)-1,:] #计算残差
res=np.array(res)
press_i.append(np.sum(res**2)) #残差平方和，并存储
press.append(np.sum(press_i)) #预测误差平方和
#-----交叉有效性检验，判断主成分是否满足条件
Q_h2[0]=1
if i>0:
Q_h2[i]=1-press[i]/ss[i-1]
if Q_h2[i]
