第十三章 DFS与BFS（保姆级教学！！超级详细的图示！！）

第十三章 DFS与BFS

• 一、深度优先搜索
• • 1、什么是DFS？
  • 2、DFS代码模板
  • • （1）问题：
    • （2）分析：
    • （3）模板：
    • 3、DFS代码分析
    • 二、广度优先搜索
    • • 1、什么是BFS？
      • 2、BFS代码模板
      • • （1）问题：
        • （2）代码：
        • 3、BFS代码分析
        • • （1）问题1：为什么要用队列？
          • （2）问题2：方向向量怎么用？
          • （3）问题3：为什么最后的输出是最短路？

            一、深度优先搜索

            1、什么是DFS？

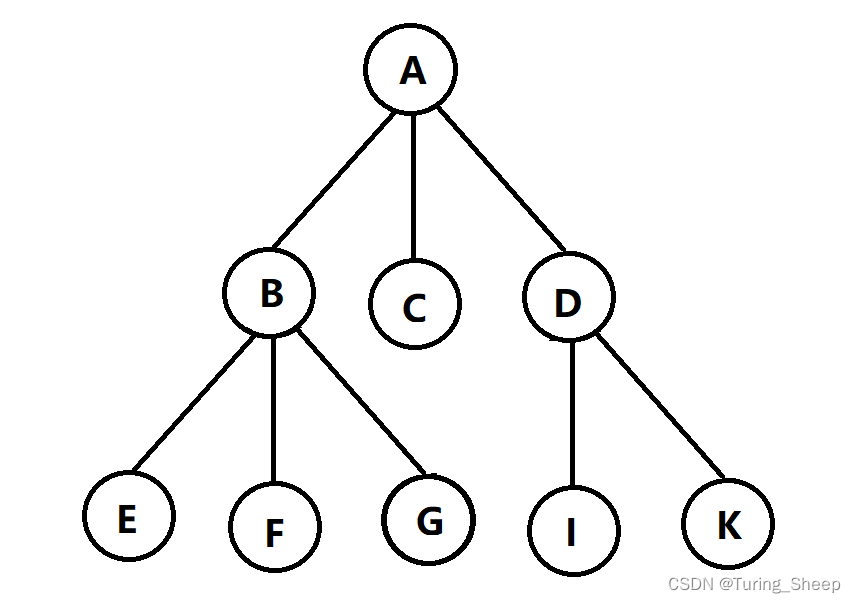
            DFS即Depth First Search，深度优先搜索。简单地理解为一条路走到黑。那么什么叫一条路走到黑呢？假设我们想在如下的地图中走出一条最长的路，那么最粗暴的方式就是枚举出每一种情况。

            

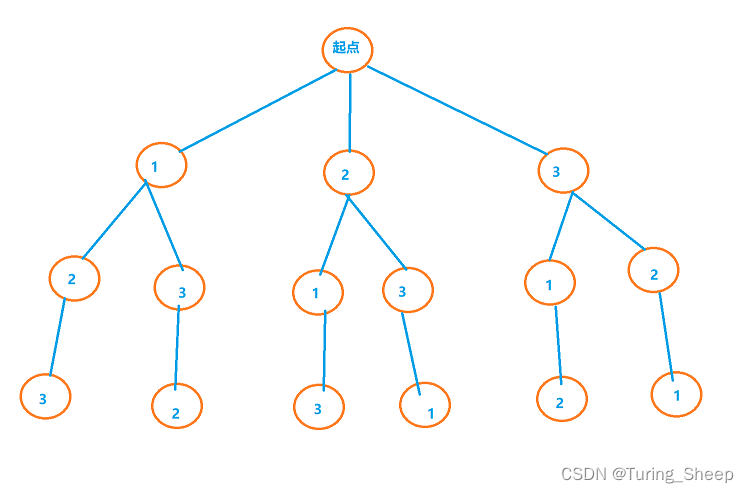
            因此，按照DFS一条路走到黑的思想，我们将会出现如下路线：

            

            先走A，然后到B，到了B有三种情况，意味着这条路还没走完，那我就接着走，从B走到E，走到E之后没路了。那我就回溯到B,为什么呢？

            因为我原本走到B的时候就有三种情况，但是刚刚只走了一种情况，因此我要回到B再去尝试第二条路，于是我们就从E回到B，然后从B去F。到了F，又没路了，那我们就回到B走第三种情况，从B到G。这样我们就走完了从A->B的三种情况。又因为在A处其实还有三种情况，因此我们走完B的三种情况后，回到A,去走除了从A->B的第二种情况，即A->C。由此以往。

            简而言之，就是我们一头扎进去，撞了南墙，我就退一步，但是决不放弃，在原基础上做出局部的改变去尝试第二条路，直到所有的情况我都试了，实在没有其他情况了，那我就回到A，从头出发，再做选择，再一头扎进去，直到成功。

            2、DFS代码模板

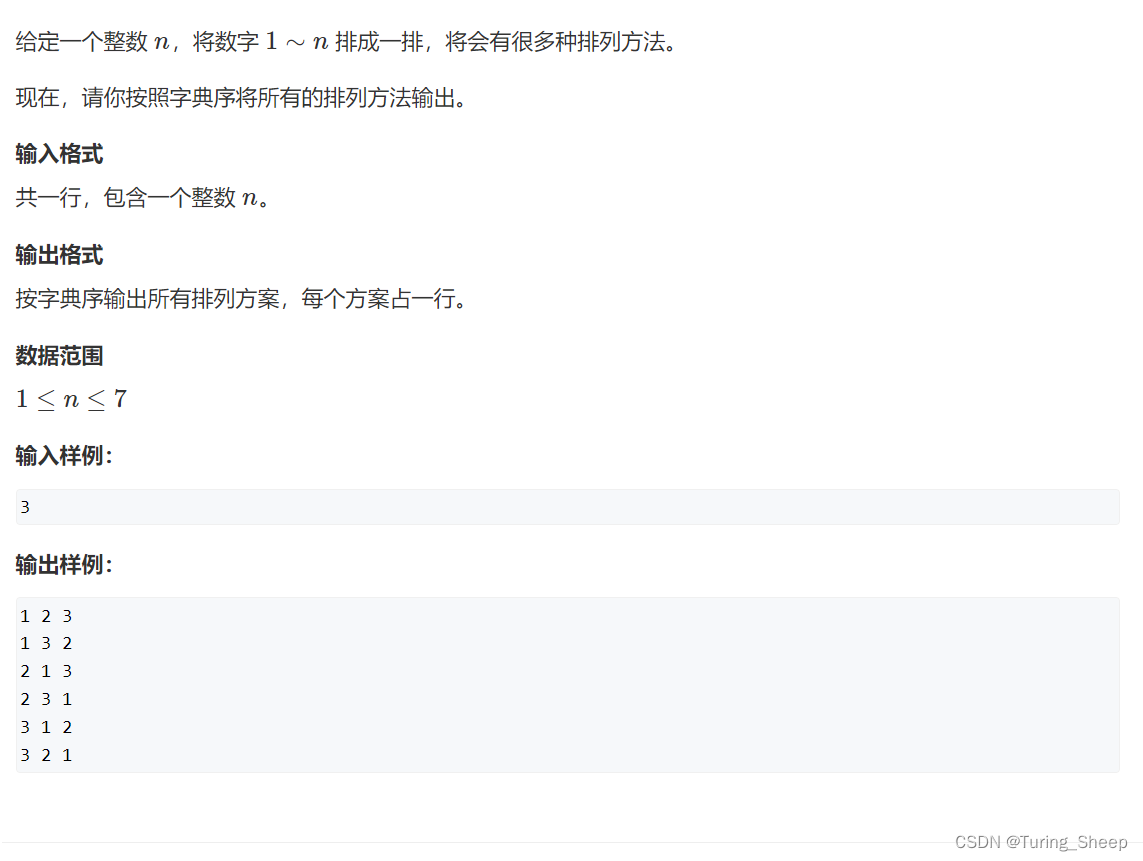
            （1）问题：

            

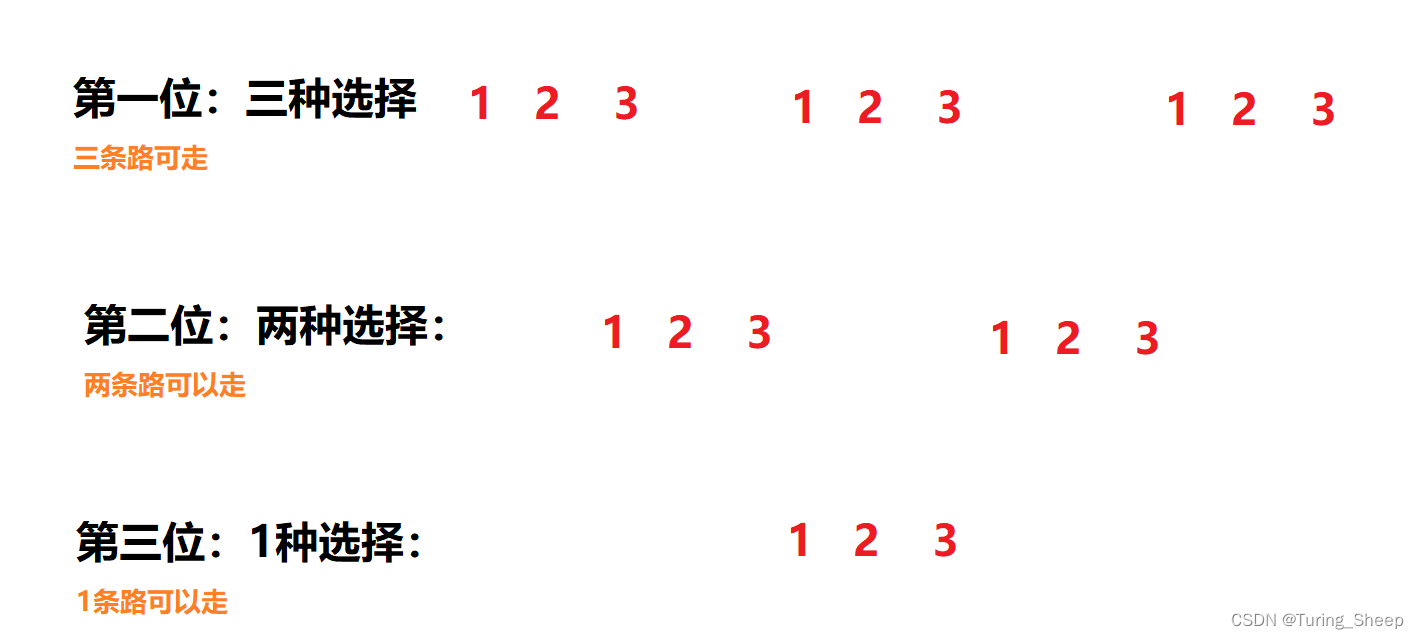
            （2）分析：

            

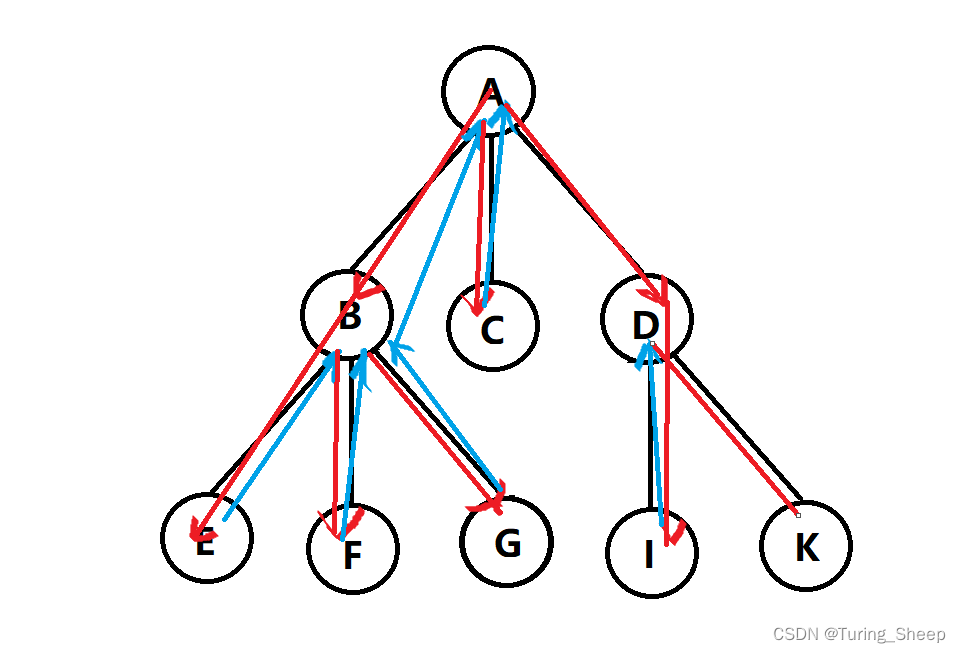
            我们将其各种选择，继续画成一棵树：

            

            这张图就清晰很多了，因此想要用DFS，我们首先要有逻辑地画出一张地图，有了地图才能去搜。

            （3）模板：

            #include
            using namespace std;
            const int N=10;
            int ans[N];
            bool mark[N];
            int n;
            void dfs(int u)
            {
                //"回头"的条件
                if(u==n)
                {
                    for(int i=0;i
                    if(mark[i]==false)
                    {
                        mark[i]=true;
                        ans[u]=i;
                        dfs(u+1);
                        //复原
                        mark[i]=false;
                        ans[u]=0;
                    }
                }
            }
            int main()
            {
                cinn;
                dfs(0);
                return 0;
            }
            -1,0,1,0},dy[4]={0,1,0,-1},n,m,ans;
            void bfs()
            {
                memset(mark,-1,sizeof mark);
                queue0,0});
                mark[0][0]=0;
                while(!q.empty())
                {
                    PII top=q.front();
                    for(int i=0;i
                        int nex=top.first+dx[i],ney=top.second+dy[i];
                        if(nex=0&&nex
                            mark[nex][ney]=mark[top.first][top.second]+1;
                            q.push({nex,ney});
                        }
                    }
                    q.pop();
                }
                cout
                cinnm;
                for(int i=0;i
                    for(int j=0;j
                        scanf("%d",&map[i][j]);
                    }
                }
                bfs();
            }