四个时间复杂度为nlogn的排序算法
三个n^2级的算法
http://t.csdnimg.cn/oQSSL
本周分享四个时间复杂度为nlogn的算法：
- 希尔排序
- 堆排序
- 快速排序
- 归并排序
1.希尔排序
1959 年 7 月，美国辛辛那提大学的数学系博士 Donald Shell 在 《ACM 通讯》上发表了希尔排序算法，成为首批将时间复杂度降到 O(n^2) 以下的算法之一。虽然原始的希尔排序最坏时间复杂度仍然是 O(n^2) ，但经过优化的希尔排序可以达到 O(n^{1.3}) 甚至 O(n^{7/6})。
希尔排序虽然现在用到的地方很少，但之所以仍然讲解，是因为理解了希尔排序之后，能够快速地其他排序算法（学习本质上是对思维的锻炼，而不是具体的知识）；
希尔排序本质上是对插入排序的一种优化，将插入排序从相邻元素的交换改变成特定下标的元素交换。它利用了插入排序的简单，又克服了插入排序每次只交换相邻两个元素的缺点。从本质上来说希尔排序是特定间隔的多次插入排序。
基本思想
● 将待排序数组按照一定的间隔分为多个子数组，对每组分别进行插入排序。（间隔分组不是取连续的一段数组，而是每跳跃一定间隔取一个值组成一组，而我们的插入排序也是对这一个间隔数组进行的插入排序）
● 逐渐缩小间隔进行下一轮排序
● 最后一轮时，取间隔为 1，也就相当于直接使用插入排序。但这时经过前面的基本排序之后，此时数组基本有序了，所以此时的插入排序只需进行少量交换便可完成
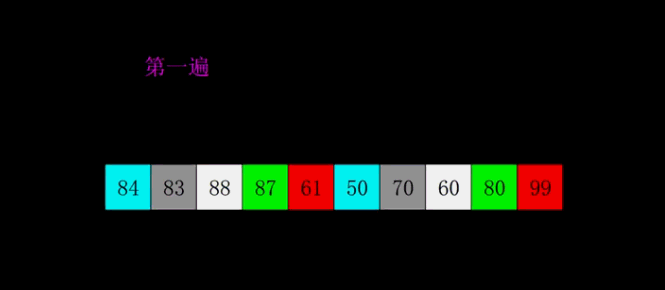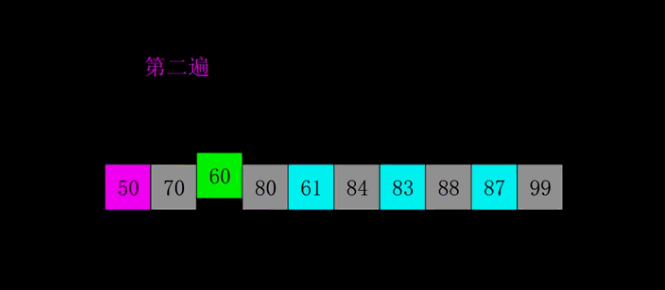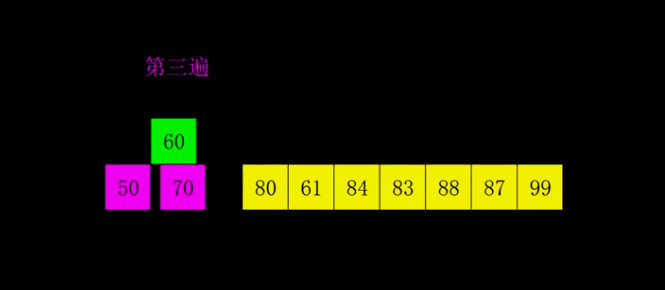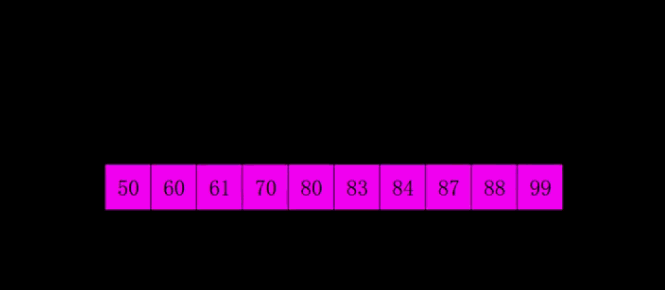
举个例子，对数组 [84, 83, 88, 87, 61, 50, 70, 60, 80, 99] 进行希尔排序的过程如下：
● 第一遍（55 间隔排序）：按照间隔 55 分割子数组，共分成五组，分别是 [84,50],[83,70],[88,60],[87,80],[61,99]。对它们进行插入排序，排序后它们分别变成： [50, 84], [70, 83], [60, 88], [80, 87], [61, 99]，此时整个数组变成 [50,70,60,80,61,84,83,88,87,99]
● 第二遍（22 间隔排序）：按照间隔 22 分割子数组，共分成两组，分别是 [50, 60, 61, 83, 87], [70, 80, 84, 88, 99]。对他们进行插入排序，排序后它们分别变成： [50, 60, 61, 83, 87], [70, 80, 84, 88, 99]，此时整个数组变成 [50,70,60,80,61,84,83,88,87,99]。这里有一个非常重要的性质：当我们完成 22 间隔排序后，这个数组仍然是保持 55 间隔有序的。也就是说，更小间隔的排序能够不断地将上一次排序的结果进行优化，使数组逐渐回归有序
● 第三遍（11 间隔排序，等于直接插入排序）：按照间隔 11 分割子数组，分成一组，也就是整个数组。对其进行插入排序，经过前两遍排序，数组已经基本有序了，所以这一步只需经过少量交换即可完成排序。排序后数组变成 [50,60,61,70,80,83,84,87,88,99]，整个排序完成。
代码实现
public static void shellSort01(int[] nums) {
//确定间隔系列 即希尔增量序列，这里是数组长度不断除以2，直到间隔为1，进行一个整体的插入排序;
for (int gap = nums.length / 2; gap >= 1; gap = gap / 2) {
//使用插入排序中的位移法对每一分组进行排序;
//插入排序的起始位置是gap,即从第一个间隔后面的元素开始,向前进行的插入排序;
for (int currentIndex = gap; currentIndex = 0 && nums[preIndex] > currentValue) {
nums[preIndex + gap] = nums[preIndex];
preIndex -= gap;
}
//这里使用preIndex+gap的原因是:如果没有进入上方的while循环，preIndex+gap = currentIndex
//如果进入了while循环，while循环都会执行preIndex-=gap的操作，这时候导致我们的下标指向了前一个间隔的函数，这时候我们需要向后移动一个间隔，指向正确的插入位置
nums[preIndex + gap] = currentValue;
}
}
}
分析
每一遍排序的间隔在希尔排序中被称之为增量，所有的增量组成的序列称之为增量序列，也就是本例中的 [5, 2, 1]。增量依次递减，最后一个增量必须为 1，所以希尔排序又被称之为「缩小增量排序」。这里的增量序列选取是通过数组长度/2，之后在这基础上不断除以2。
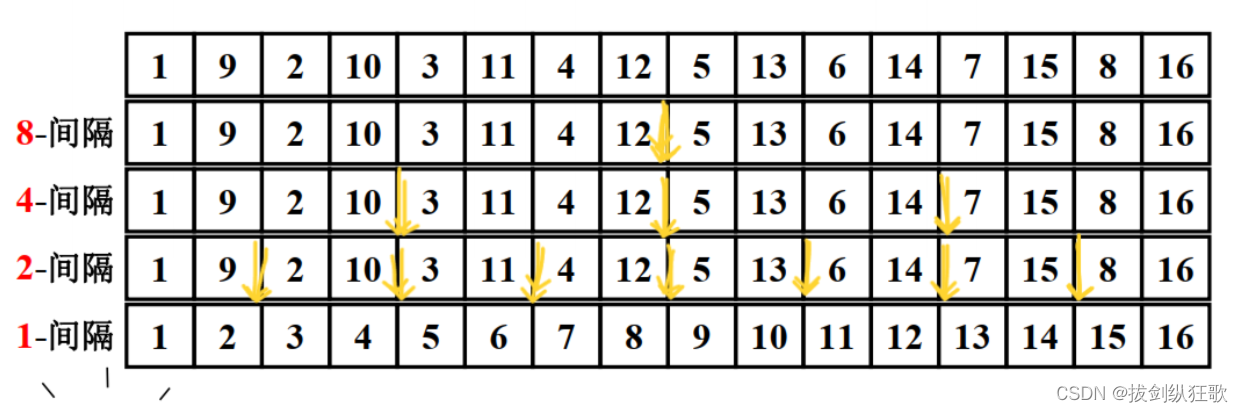
增量序列的选定会极大地影响希尔排序的效率。增量序列如果选得不好，希尔排序的效率可能比插入排序效率还要低，举个例子：
像这一个例子，以8、4、2为间隔的排序都没有起作用，真正对起作用的是1间隔的排序，这时候的时间复杂度要大于直接使用插入排序的时间复杂度。
原因就在于，我们选择的增量序列之间存在着公因子，不互相为质数，这样导致小的增量根本不起作用，在排序时出现一些不必要的重复操作，从而影响排序算法的性能。
一般来说，为了保证希尔排序的效率，我们希望选择的增量序列中的元素是互质的，这样可以最大程度地减少不必要的比较和交换操作，提高排序的效率。
代码优化
这里推荐增量选取使用 knuth 增量序列：D_1 = 1; D_{k+1} = 3 * D_k + 1，也就是 1,4,13,40,...，数学界猜想它的平均时间复杂度为 O(n^{3/2})；
使用 Knuth 序列进行希尔排序的代码如下：
public static void shellSortByKnuth(int[] arr) {
// 找到当前数组需要用到的 Knuth 序列中的最大值
int maxKnuthNumber = 1;
while (maxKnuthNumber 0; gap = (gap - 1) / 3) {
// 从 gap 开始，按照顺序将每个元素依次向前插入自己所在的组
for (int i = gap; i = 0 && currentNumber
时间-空间复杂度分析
时间复杂度分析：希尔排序时间复杂度非常难以分析，它的平均复杂度界于 O(n) 到 O(n^2) 之间，普遍认为它最好的时间复杂度为 O(n^{1.3})。不同的增量序列会有不同的时间复杂度。
空间复杂度：采用的都是常数级的临时变量，所以空间复杂度为O（1）
堆排序
前置知识
堆：符合以下两个条件之一的完全二叉树：
● 根节点的值 ≥ 子节点的值，这样的堆被称之为最大堆，或大顶堆；
● 根节点的值 ≤ 子节点的值，这样的堆被称之为最小堆，或小顶堆。
完全二叉树：
若一棵二叉树的所有叶子节点都在最后一层或者倒数第二层，并且最后一层的叶子节点左边连续，倒数第二层的叶子节点右边连续，则我们称此二叉树为完全二叉树。
● 对于完全二叉树中的第 i 个数，它的左子节点下标：left = 2i + 1
● 对于完全二叉树中的第 i 个数，它的右子节点下标：right = left + 1
● 对于有 n 个元素的完全二叉树(n≥2)(n≥2)，它的最后一个非叶子结点的下标：n/2 - 1（n为对应数组的长度）
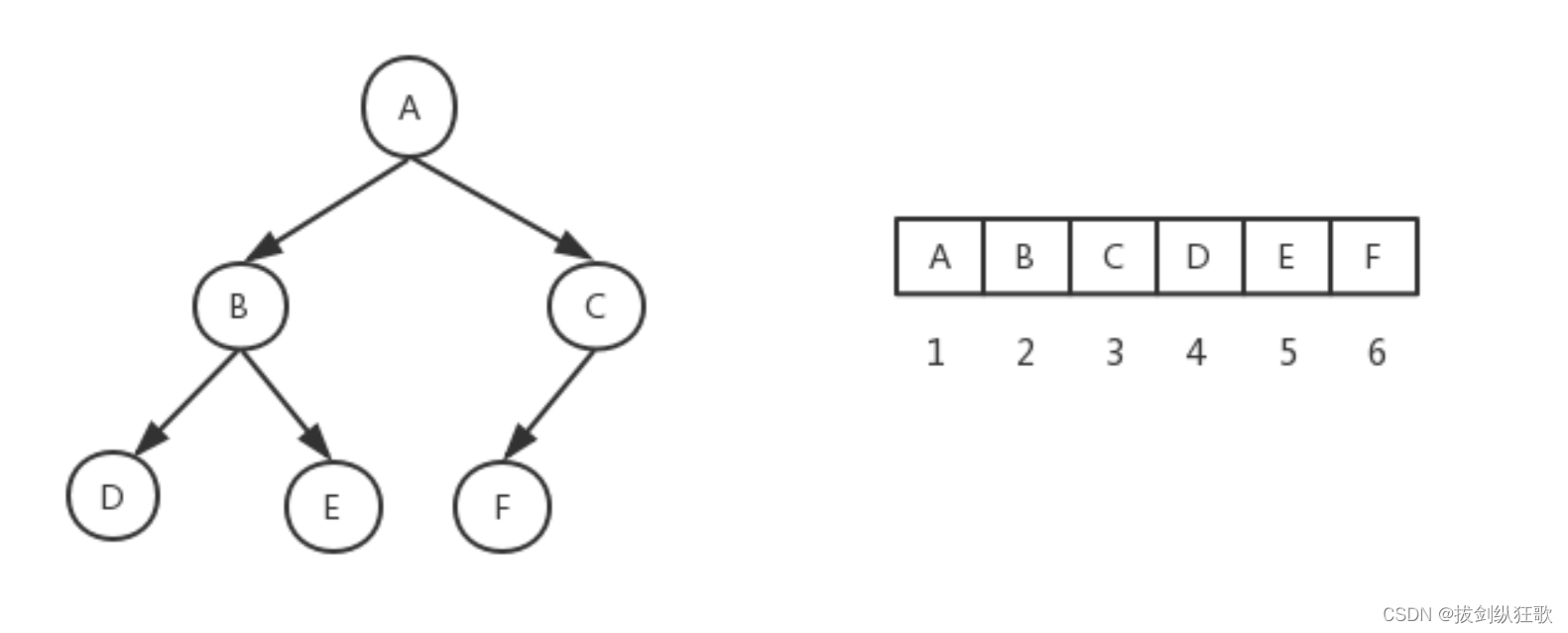完全二叉树与数组的对应关系图
基本思想
1. 用数组构建出一个大顶堆，取出堆顶的数字；
2. 调整剩余的数字，构建出新的大顶堆，再次取出堆顶的数字；
3. 循环往复，完成整个排序。
堆排序并不是使用二叉树进行排序，而是在使用数组去模拟二叉树的结构，是一些特定的数组范围进行排序。
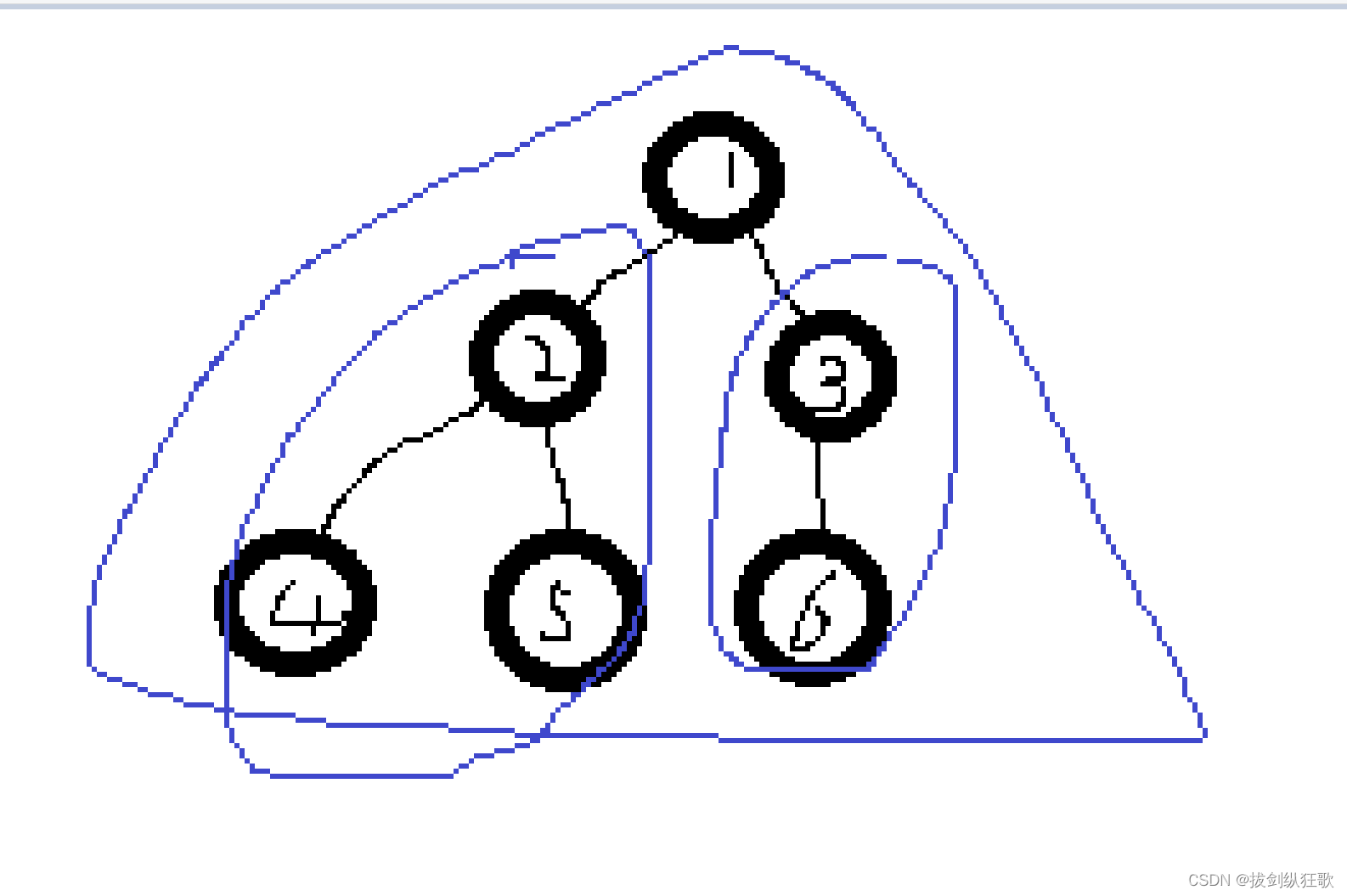
构建大顶堆的过程是很多初学者不明白的，其实大顶堆的构建非常简单，我们可以将这个数组的初始状态看成是一个完全二叉树，从最后一个非叶子节点开始自下而上地构建大顶堆，当我们依次向上将每一个子树都构建成大顶堆，构建到根节点的时候，数组最终形成了一个大顶堆结构。
如图所示，我们构建以3为根节点的大顶堆，再构建以2为根节点的大顶堆，最后构建以1为节点的大顶堆。其实，这一个过程就是我们的基本思想中第二步，调整剩余数组，重新构建大顶堆。值得注意的是，我们在进行大顶堆构架的时候，一定要注意交换元素后的对于其左右子树的影响，一定要保持住大顶堆的结构。
动图演示如下：
代码实现
public class heapSortDemo {
public static void main(String[] args) {
int[] nums = {5, 0, 1, 9};
heapSort(nums);
System.out.println(Arrays.toString(nums));
}
public static void heapSort(int[] nums) {
// 1.构建大顶堆
constructMaxHeap(nums);
/* 2.大顶堆构建完成，之后将堆顶元素依次同末尾元素进行交换即可。
注意：一旦发生了交换，构建大堆顶一定是有范围的，不再是全体数组了,不然永远都是值比较大的元素同其叶子节点的元素进行交换;*/
for (int i = nums.length - 1; i >= 0; i--) {
swap(nums, 0, i);
maxHeapify(nums, 0, i);
}
}
/**
* 构建堆的过程就是实现一个特定结构的降序排列 类似于希尔排序
* 我们采用自下而上的构建方式，从二叉树的最后一个非叶子节点开始构建
* 构建的过程注意，后一次元素交换后，对于其叶子节点的影响，要同叶子节点进行比较。
*/
public static void constructMaxHeap(int[] nums) {
for (int i = nums.length / 2 - 1; i >= 0; i--) {
maxHeapify(nums, i, nums.length);
}
}
/**
* 堆中每一个节点的初始化操作，以节点、子树为单位堆的构建。
* 这是一个根据当前的节点，构建最大堆的方法
* @param nums 待排序的数组
* @param currentIndex 当前构建堆的下标
* @param heapSize 本次排序的数组范围
*/
public static void maxHeapify(int[] nums, int currentIndex, int heapSize) {
int leftIndex = 2 * currentIndex + 1;
int rightIndex = 2 * currentIndex + 2;
// 记录根结点、左子树结点、右子树结点三者中的最大值下标
int largest = currentIndex;
// 与左子树结点比较
if (leftIndex nums[largest]) {
largest = leftIndex;
}
// 与右子树结点比较
if (rightIndex nums[largest]) {
largest = rightIndex;
}
if (largest != currentIndex) {
// 将最大值交换为根结点
swap(nums, currentIndex, largest);
// 再次调整交换数字后的大顶堆
maxHeapify(nums, largest, heapSize);
}
}
public static void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
分析
大顶堆构建完成之后，堆顶元素同末尾元素的交换，一定要进行数组范围的缩减，这里是使用heapSize进行控制的。
时间-空间复杂度
堆排序总的时间复杂度为 O(nlogn)。
堆排序的空间复杂度为 O(1)，只需要常数级的临时变量。
堆排序和选择排序一样，是对数组进行部分排序，每次排好一个最大值或者最小值。适合寻找第几大的值这样的算法。
快速排序
快速排序算法由 C. A. R. Hoare 在 1960 年提出。它的时间复杂度也是 O(nlogn)，但它在时间复杂度为 O(nlogn) 级的几种排序算法中，大多数情况下效率更高，所以快速排序的应用非常广泛。再加上快速排序所采用的分治思想非常实用，使得快速排序深受面试官的青睐，所以掌握快速排序的思想尤为重要。
基本思想
1. 从数组中取出一个数，称之为基数（pivot）
2. 遍历数组，将比基数大的数字放到它的右边，比基数小的数字放到它的左边。遍历完成后，数组被分成了左右两个区域
3. 将左右两个区域视为两个数组，重复前两个步骤，直到排序完成
pivot中文意思是轴，每一次数组的遍历就是把基数左边的数字大于基数的数字，旋转到右边；把基数右边小于基数的数字旋转到左边，形成一个基数左边都小于等于基数，右边都大于基数的数组结构。【pivot的选取是快速排序算法的核心，快速排序算法的优化也都大都围绕着pivot轴的选取和pivot的增加进行。所谓双轴快排就是一次选取两个基数，将数组分为三个区域进行旋转】
对于pivot轴的选择：
基数的选择没有固定标准，随意选择区间内任何一个数字做基数都可以。
通常来讲有三种选择方式：
● 选择第一个元素作为基数 【入门推荐，方便理解，本文依次为例】
● 选择最后一个元素作为基数
● 选择区间内一个随机元素作为基数 【优化推荐，降低最坏情况出现的概率】
代码实现
public class quickSortDemo {
public static void main(String[] args) {
int[] nums = {6, 2, 1, 3, 5, 5, 1, 4};
// 为了方便调用，书写的重载方法
quickSort(nums);
System.out.println(Arrays.toString(nums));
}
public static void quickSort(int[] nums) {
quickSort(nums, 0, nums.length - 1);
}
public static void quickSort(int[] nums, int start, int end) {
//什么时候退出递归，当本次快速排序的数组元素个数为0或者为1的时候，文章下方有解释
if (start >= end) return;
int middle = partitionRandom(nums, start, end);
quickSort(nums, start, middle - 1);
quickSort(nums, middle + 1, end);
}
// 将 待排序数组arr 从 start 到 end 分区，左边区域比基数小，右边区域比基数大，然后返回中间值的下标
public static int partition(int[] arr, int start, int end) {
// 取第一个数为基数
int pivot = arr[start];
// 从第二个数开始分区,左边界
int left = start + 1;
// 右边界
int right = end;
// left、right 相遇时退出循环
while (left
分析
对于递归退出的边界，这里为什么是start >= end呢？
递归的数组元素个数为0或者为1的时候退出递归。因为这时候进行任何排序都是没有任何意义的。最原始的条件应该是下方代码这样的。
public static void quickSort(int[] nums, int start, int end) {
int middle = partitionRandom(nums, start, end);
// 当左边区域中至少有 2 个数字时，对左边区域快速排序
if(start != middle && start != middle-1) quickSort(nums, start, middle - 1);
// 当右边区域中至少有 2 个数字时，对右边区域快速排序
if(end != middle+1 && end != middle) quickSort(nums, middle + 1, end);
}
我们对边界进行简化：
- 当进行左边区域的递归时
如果start == middle 表示将要递归的数组范围内元素的个数为0；
如果start == middle-1表示将要递归的数组范围内元素的个数为1 ；
我们带着这样的条件进入递归中，可以得出start和end的关系
当start == middle时，进行递归后，start=start,middle-1=end---> start = end+1;
当start == middle-1时，进入递归后，start=start,end=middle-1--->start = end;
- 当进行右边区域的递归时
如果end == middle 表示将要递归的数组范围内元素的个数为0；
如果end == middle+1 表示将要递归的数组范围内元素的个数为1；
我们带着这样的条件进入递归中，可以得出start和end的关系
当end== middle时，进行递归后，start=middle+1,end=end---> start = end+1;
当end == middle+1时，进入递归后，start=middle+1,end=end--->start = end;
综上所述，进入递归后的终止条件可以改变成 start！=end || start！=end+1。
根据我们的程序设定，middle>=start&&middle=right就退出递归。由于我们是在下一次递归中进行这一系列的推理。递归的终止条条件应该放到partition前面，递归退出的条件改变为
● start == end: 表明区域内只有一个数字
● start == end + 1: 表明区域内一个数字也没有，
public static void quickSort(int[] arr, int start, int end) { // 如果区域内的数字少于 2 个，退出递归 if (start >= end) return; // 将数组分区，并获得中间值的下标 int middle = partition(arr, start, end); // 对左边区域快速排序 quickSort(arr, start, middle - 1); // 对右边区域快速排序 quickSort(arr, middle + 1, end); }优化
双指针分区算法
public static int doublePointerPartition1(int[] arr, int start, int end) { int pivot = arr[start]; int left = start + 1; int right = end; while (left
- 当进行右边区域的递归时
