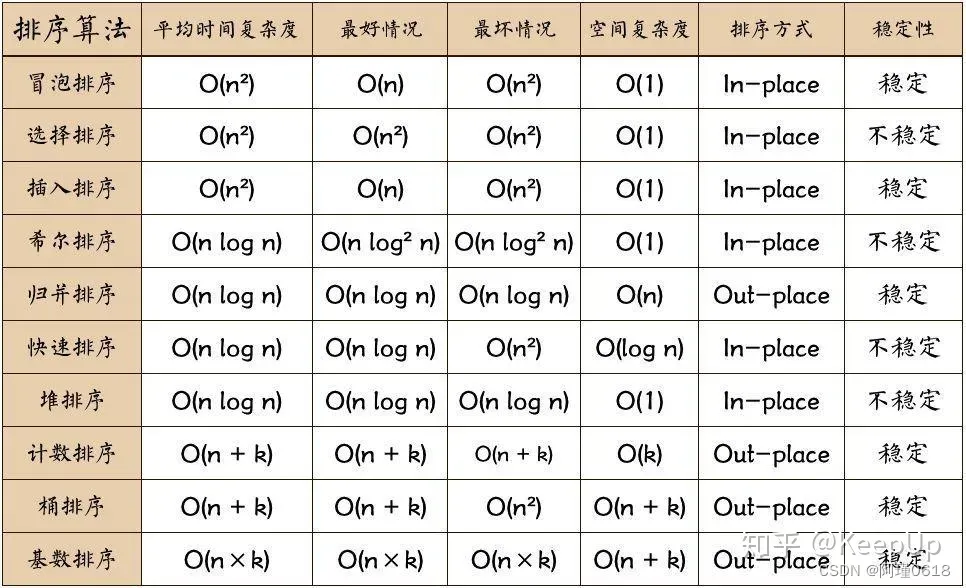
【数据结构】常见八大排序算法(附动图)
一、前言
关于排序,有一些术语,例如算法的稳定/不稳定,内排序和外排序等,需要我们了解一下
稳定:当未排序时a在b前面且a=b,排序后a仍然在b前面
不稳定:当未排序时a在b前面且a=b,排序后a可能会出现在b后面
内排序:数据记录在内存中进行排序
外排序:由于数据太大,在排序过程中需要访问外存
二、冒泡排序
冒泡排序的效率十分低下,但是胜在排序过程形象易懂,适用于教学使用。
通过对数列的遍历并比较相邻的元素,将目标元素逐步移动到数组的尾端,就像泡泡慢慢冒出水面,因此得名。
2.1 算法描述
(1)从头到尾比较相邻元素,如果第一个大于第二个(升序)就将二者交换位置
(2)重复n-1遍第一步(最后一个元素一定是最小的所以不用排了)
2.2 动图展示
2.3 代码实现
void BubbleSort(int* a, int n) //冒泡排序
{
for (int i = 0; i a[j])
{
int tmp = a[j]; //交换元素
a[j] = a[j - 1];
a[j - 1] = tmp;
}
}
}
}
2.4 算法优化
如果遍历一遍数组后没有发生任何元素交换,说明数组已经有序,排序就可以结束了。
优化后的代码如下:
void BubbleSort(int* a, int n) //冒泡排序
{
for (int i = 0; i a[j])
{
int tmp = a[j];
a[j] = a[j - 1];
a[j - 1] = tmp;
flag = true; //如果发生元素交换,flag赋值为true
}
}
if (flag == false) //如果单趟冒泡后flag没有发生改变说明已经有序
break;
}
}
三、选择排序
选择排序是表现最稳定的算法之一,但它的效率也很低下,无论情况的好与坏它的时间复杂度都是O(n2)。
3.1 算法描述
(1)遍历未排序的部分找出最小值(升序),将其与未排序部分的第一个元素交换
(2)重复n-1遍第一步(最后一个元素一定是最大的所以不用排了)
3.2 动图展示
3.3 代码实现(优化版)
上面的动图中每次遍历只寻找最小值,我们可以优化一下,每次遍历同时寻找最大值和最小值。
void SelectSort(int* a, int n) //选择排序
{
int begin = 0, end = n - 1;
int tmp = 0;
while (begin
四、插入排序
插入排序的逻辑十分简单,将待排序的元素一个个插入到一个已经排好序的有序数列中,直到整个数列都有序为止。
过年的时候我们打扑克牌,将一堆无序的牌变得有序的过程实际上就是运用了插入排序的思想。
4.1 算法描述
(1)只有一个元素时默认有序,所以我们跳过第一个元素
(2)取出下一个元素,在已经排好序的序列中从后向前扫描并与取出的元素对比
(3)如果扫描到的元素大于取出的元素(升序),就将扫描的元素向后移一位
(4)重复步骤3,直到扫描到的元素小于或等于取出的元素,将取出的元素放入有序数列
(5)重复步骤2~5
4.2 动图展示
4.3 代码实现
void InsertSort(int* a, int n) //插入排序
{
for (int i = 1; i = 0) //扫描有序序列
{
if (tmp
五、希尔排序
希尔排序又称缩小增量排序,它也是插入排序的一种,由希尔(Donald Shell)于1959年提出,也是时间复杂度冲破O(n2)的第一批算法之一。
5.1 算法描述
(1)设定一个gap,并按照gap将待排序数列分割成若干子序列,对子序列分别进行插入排序
(2)将gap缩小,重复步骤1,当gap=1时就是插入排序
5.2 动图展示
5.3 代码实现
void ShellSort(int* a, int n) //希尔排序
{
int gap = n;
while (gap > 1)
{
gap = gap / 3 + 1;
for (int i = 0; i = 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end -= gap;
}
else
break;
}
a[end + gap] = tmp;
}
}
}
希尔排序是对插入排序的优化,当gap>1时都是预排序,目的是让数组不断趋近有序;当gap为1时数组已经很接近有序了,所以排起来就会很快。
六、堆排序
堆排序(Heapsort)是指利用堆积树(堆)这种数据结构所设计的一种排序算法,是选择排序的一种,通过堆来进行选择数据。
在前面学习数据结构堆的时候我们已经见过堆排序了,这里不再赘述。
6.1 算法描述
(1)先建堆,升序建大堆,降序建小堆
(2)将堆顶元素与堆尾元素互换,并排除出堆
(3)此时堆的性质被打破,通过向下调整算法调整为新的堆,重复操作2直至序列有序
6.2 动图展示
6.3 代码实现
typedef int HPDataType;
typedef struct Heap
{
HPDataType* arr;
int size;
int capacity;
}Heap;
void AdjustDown(int* a, int n, int root) //向下调整算法
{
int child = root * 2 + 1;
while (child a[child])
{
child = child + 1;
}
if (a[child] > a[root])
{
HPDataType tmp = a[child];
a[child] = a[root];
a[root] = tmp;
root = child;
child = root * 2 + 1;
}
else
{
break;
}
}
}
void HeapSort(int* a, int n) //堆排序
{
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i); //通过向下调整算法建堆
}
while (n > 1)
{
int tmp = a[0]; //将堆顶元素交换到堆尾
a[0] = a[n - 1];
a[n - 1] = tmp;
n--; //排除原堆顶元素
AdjustDown(a, n, 0); //调整被打乱的堆
}
}
七、快速排序
快速排序是本文的重头戏,它是对冒泡排序的一种改进算法,在当前所有的内部排序算法中,快速排序被认为是最好的排序算法之一。
7.1 算法描述
(1)任选待排序序列中的某元素作为基准值,按照该值通过单趟排序将待排序的序列分为左右两个子序列,左子序列中的元素均小于基准值,右子序列中的元素均大于基准值(升序)
(2)分别对左右两个子序列重复步骤1,直至序列有序
7.2 单趟排序的实现
不同版本的快排核心思想都是一样的,区别在于单趟排序的方式不同
7.2.1 hoare版本
大体思路
(1)选定待排序序列头部(或尾部)的元素作为key值,保存下标
(2)扫描待排序序列,一个从左到右寻找比key大的值,另一个从右向左寻找比key小的值,找到后将二者交换。
(3)当待排序序列扫描结束后,将序列头部的key与left位置处的元素交换,并返回left(此时left是key值的下标)
动图展示
代码实现
int PartSort(int* a, int left, int right) //单趟排序hoare版本
{
//left从待排序序列头部向后走,right从待排序序列尾部向前走
int key = left; //将待排序序列的第一个元素作为key值
while (left = a[key]) //right位置的值不比key小时向前走
{
right--;
}
while (left
7.4 非递归实现快排
非递归的方式需要用到栈,通过对待排序区间下标的压栈和出栈来实现快排
大体思路
(1)首先将待排序序列尾部的下标压入栈中,再将头部的下标压入栈中(因为后面出栈要先取出头部再取出尾部,栈的特性是后进先出)
(2)取两次栈顶元素,分别取出序列头部和尾部的下标,对这一区间进行单趟排序后获取key值的下标
(3)当key值不与原区间头部或尾部相邻时,以key值为分界将先前的区间拆分成两部分,分别压入栈中
(4)重复步骤2~3直到栈为空
代码实现
void QuickSortNonR(int* a, int left, int right) //非递归实现快排
{
Stack st;
StackInit(&st);
StackPush(&st, right);
StackPush(&st, left);
while (!StackEmpty(&st))
{
int begin = StackTop(&st);
StackPop(&st);
int end = StackTop(&st);
StackPop(&st);
int keyi = PartSort2(a, begin, end);
if (keyi + 1
具体关于栈的实现可以前往 数据结构——栈-CSDN博客 查看
7.5 算法优化
(1)三数取中法
快速排序虽然效率高,但是还是有缺陷的。
当快排在排序大量有序或者接近有序的序列时,选择的key容易恰好为最小值,效率比较低下,会进行一些不必要的递归。
当递归调用层数过深,会导致栈溢出的情况,这里我们可以使用三数取中的办法来对这种情况进行优化。
三数取中,就是对比待排序序列头部的值、中部的值和尾部的值,选出三者中既不是最大也不是最小的值作为key值,并放到序列头部
其代码实现如下:
int GetMidIndex(int* a, int left, int right)//三数取中
{
int mid = (left + right) / 2;
if (a[left] > a[mid])
{
if (a[mid] > a[right])
return mid;
else if (a[left] > a[right])
return right;
else
return left;
}
else
{
if (a[mid]
具体的使用,我们只需要在单趟排序代码的开头加上这么一段就行:
int midi = GetMidIndex(a, left, right);
tmp = a[left];
a[left] = a[midi];
a[midi] = tmp;
(2)小区间优化
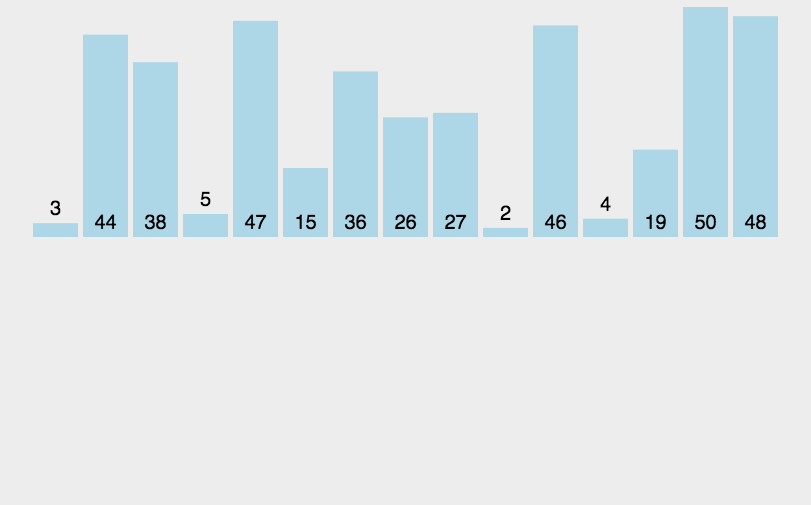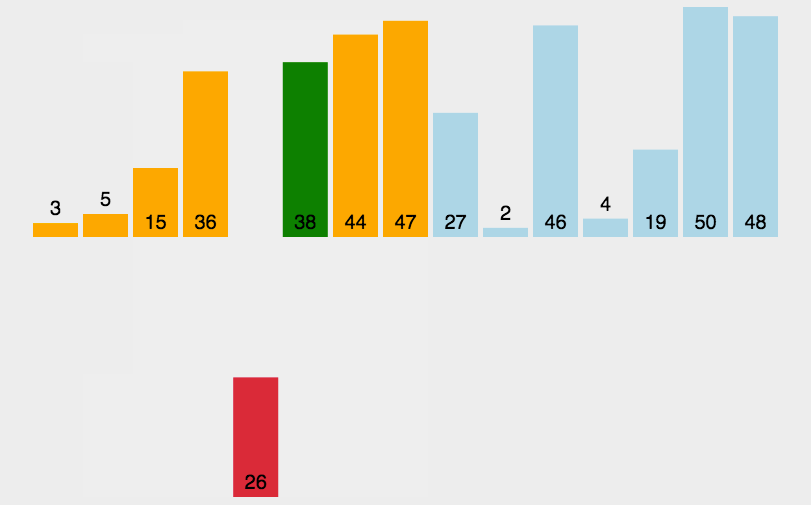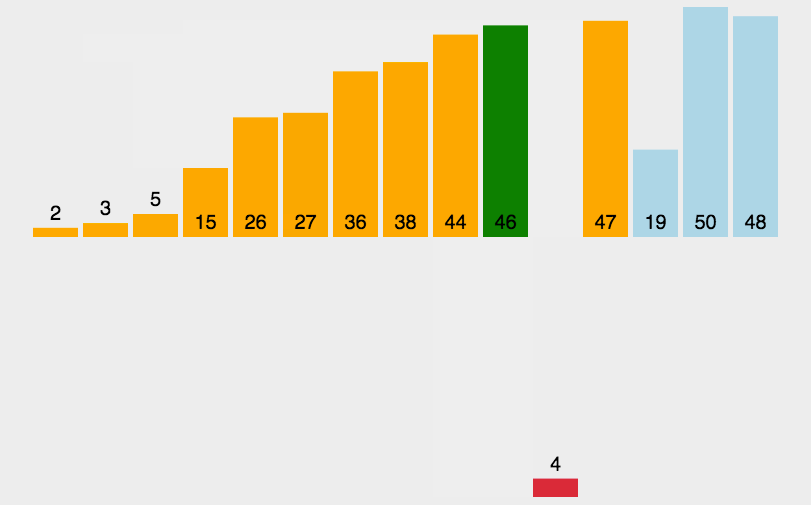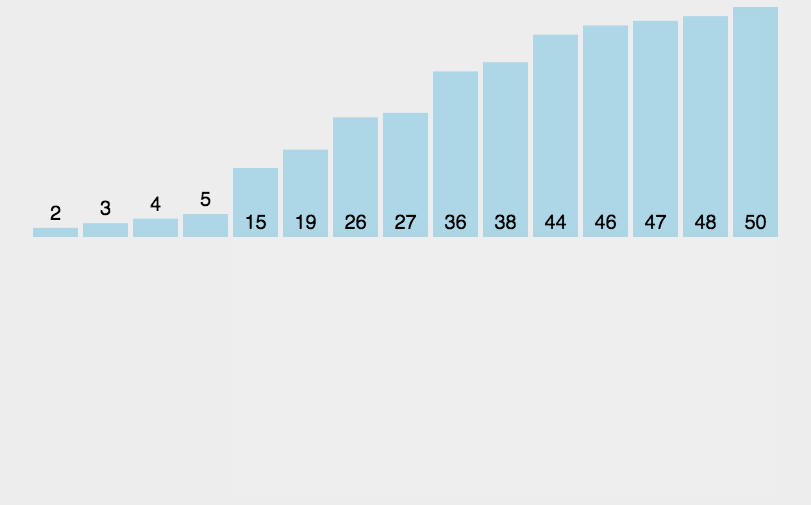
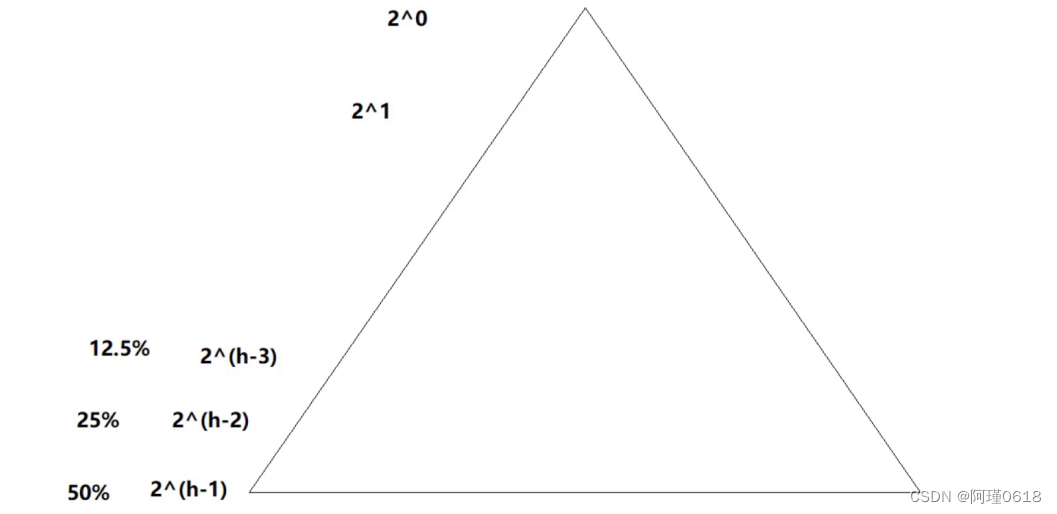
快排在排序一个数据量为100万的无序序列时只需要递归20层,但排序一个8个数据的无序序列时就要递归3层。
在递归出的二叉树结构中,最底部的三层的递归次数竟然占用了全部递归次数的87.5%!
因此我们可以对递归实现快排的代码进行优化,当区间的数据量较小时,转为使用其他的排序算法
本质上是为了减少递归调用次数来提高效率
这里我们可以使用插入排序来排序数据量较小的区间
void QuickSort(int* a, int left, int right) //小区间优化版快排
{
if (left >= right)
return;
if (right - left + 1
小区间优化的思想对递归实现归并排序也tong'yang'sh
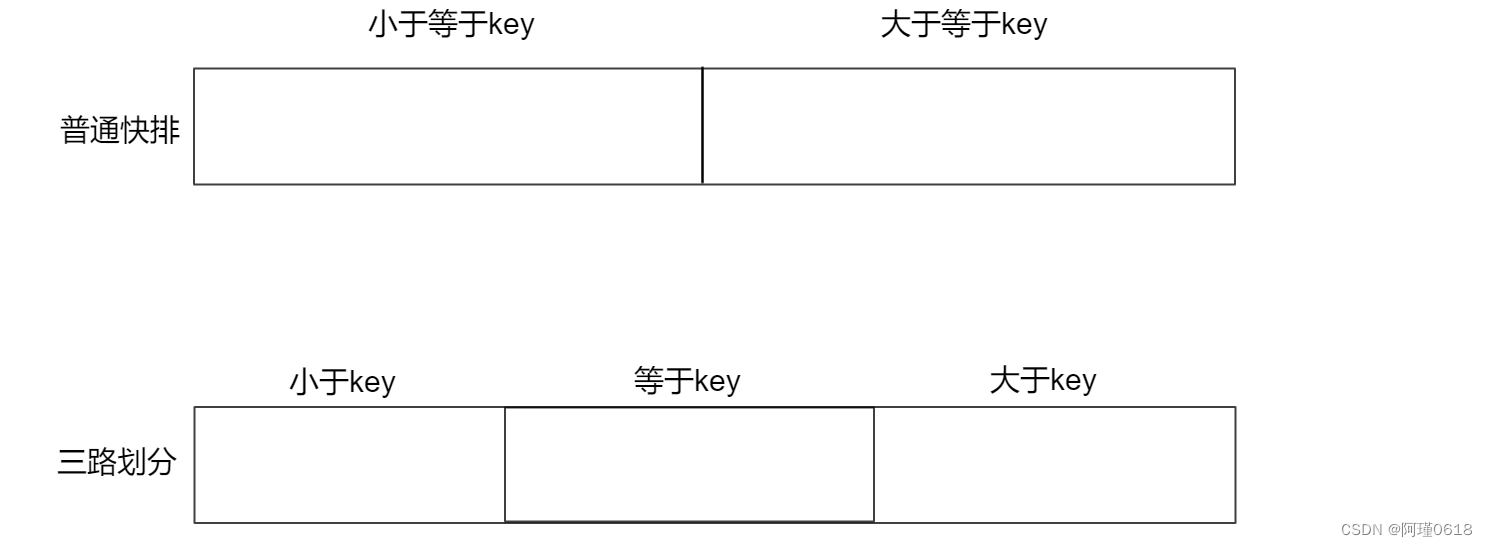
(3)三路划分
虽然三数取中法能解决待排序序列有序或接近有序的情况,但是如果序列中有大量的元素和key相等,甚至整个序列所有元素都相等时,三数取中也无法解决这种情况
这时需要使用三路划分的思想
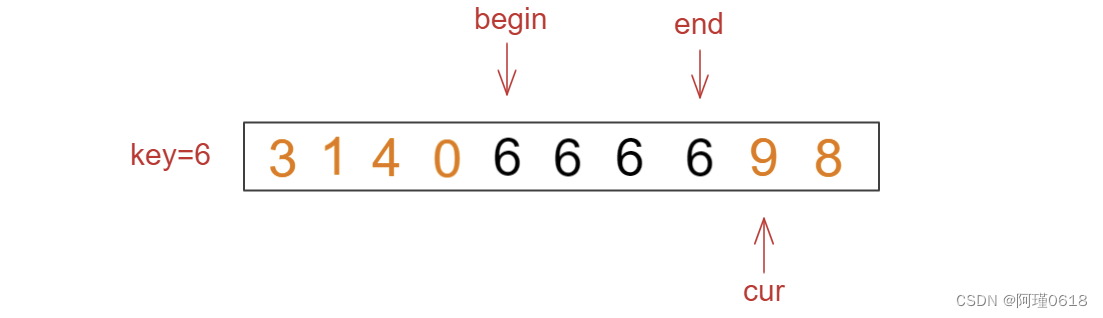
三路划分的大体思路:
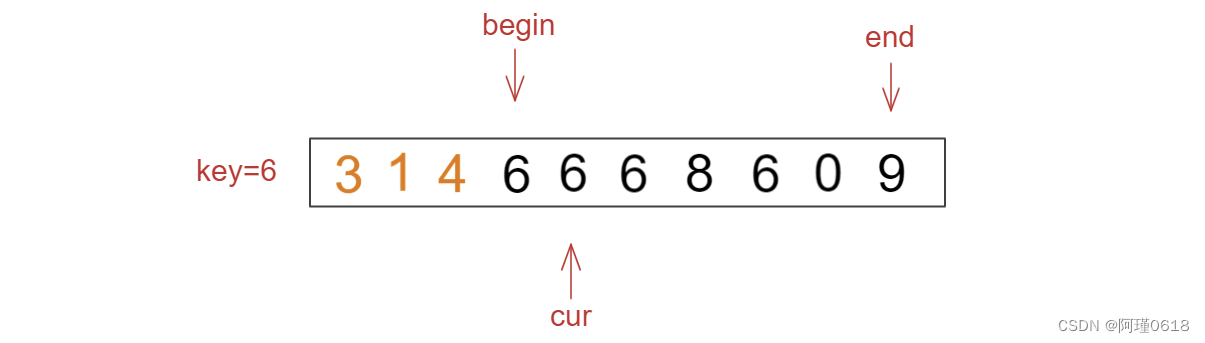
(1)begin指向区间头部,cur指向begin的下一个位置,end指向区间尾部,以头部元素作为key
(2) 如果cur处的值小于key,则将begin和cur处的元素交换,二者各向后一步
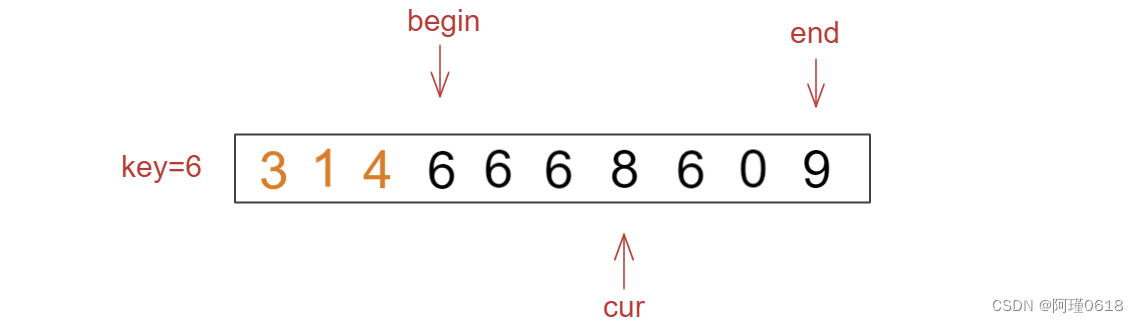
(3)如果cur处的值等于key,则cur向后走一步
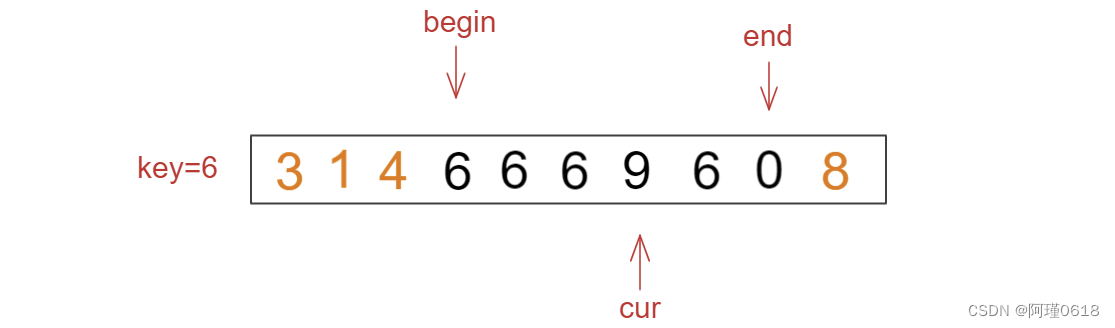
(4)如果cur处的值大于key,则将cur和end处的元素交换,cur向前走一步
(5)重复以上步骤直到cur > end时结束
(6)对左边小于key的部分和右边大于key的部分进行递归
三路划分的代码实现:
void QuickSortThreeWay(int* a, int left, int right)//三路划分版快排
{
if (left >= right)
return;
int begin = left;
int end = right;
int cur = begin + 1;
int key = a[left];
while (cur key)
{
Swap(&a[cur], &a[end]);
end--;
}
else
{
cur++;
}
}
QuickSort(a, left, begin - 1);
QuickSort(a, end + 1, right);
}
八、归并排序
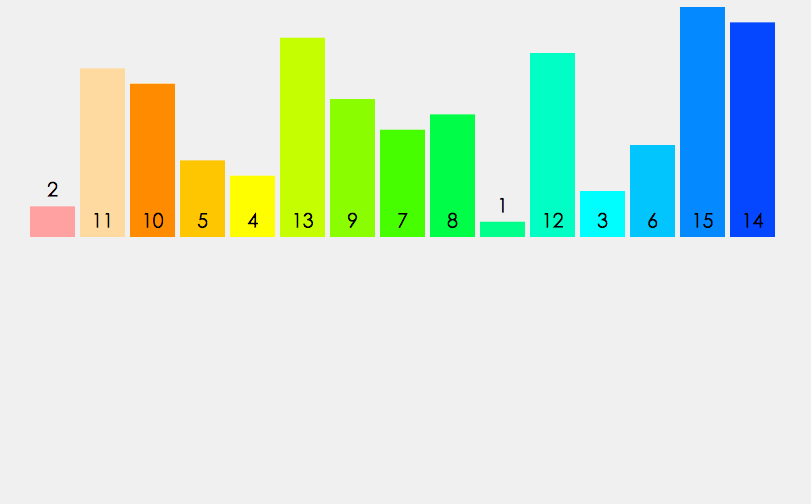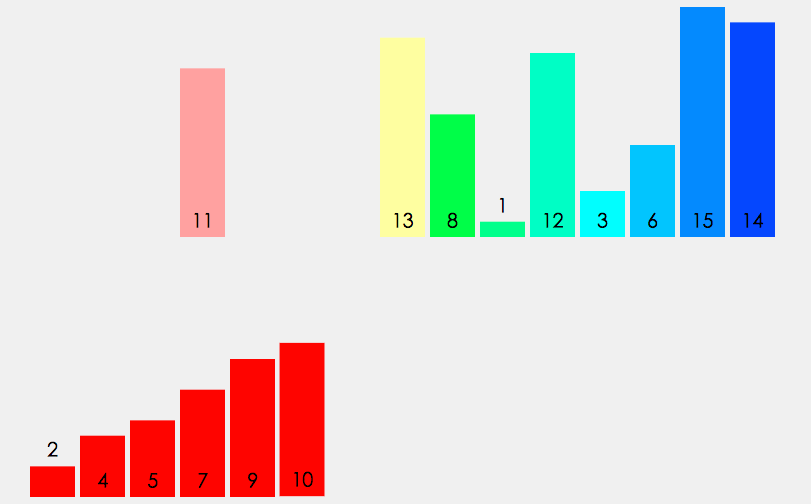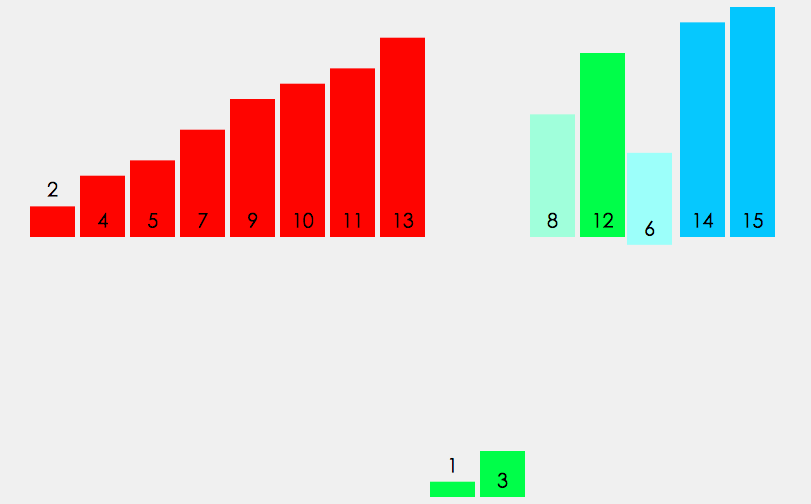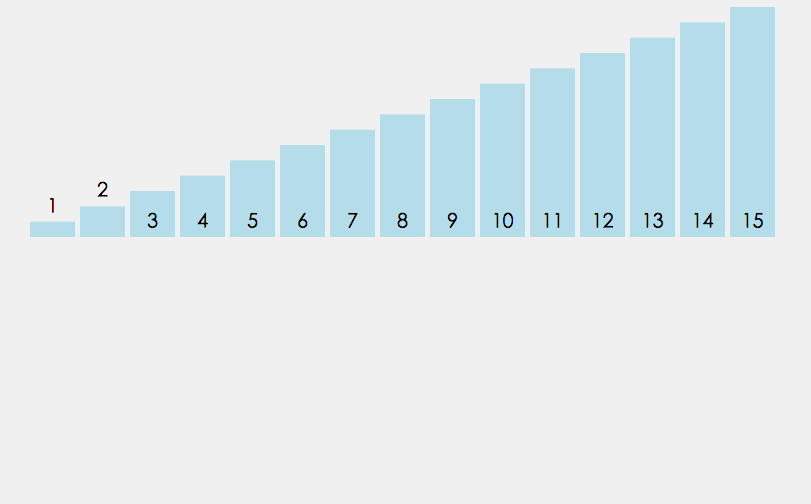
归并排序的核心思想:分治
分治就是将一个复杂的问题分解成子问题,子问题再分解成更小子问题,直到最后子问题可以简单求解。在求二叉树的节点个数和二叉树的高度时我们也使用过这个思想。
将待排序的序列分解为两个子序列,再将子序列继续分解,直到每个子序列中只有一个元素,此时默认有序。再将有序的子序列逐渐归并到一起。
若将两个有序子序列合并成一个序列,称为二路归并。归并排序的逻辑图如下:
8.1 算法描述
(1)malloc一块和待排序序列大小相同的空间,用来临时存放归并后的序列
(2)通过递归或迭代将待排序序列拆分多个子序列
(3)子序列间两两归并到开辟出的空间中,具体操作可以参考两个有序数组合并
(4)将归并后的子序列用memcpy覆盖到原序列中
(5)重复上述操作直到序列有序
8.2 动图展示
8.3 递归实现归并排序
大体思路
(1)通过递归将待排序序列不断的对半分,直到分出的子序列中只有一个元素
(2)计算出相邻两个子序列区间的边界,对二者进行归并
代码实现
我们不能每次递归都开辟一次空间,所以需要将主要的代码都放在子函数中,对子函数进行递归
//递归实现归并排序
void _MergeSort(int* a, int begin, int end, int* tmp)
{
if (begin == end)
return;
int midi = (begin + end) / 2;
_MergeSort(a, begin, midi, tmp);
_MergeSort(a, midi + 1, end, tmp);
int begin1 = begin, end1 = midi;
int begin2 = midi + 1, end2 = end;
int i = begin;
while (begin1