时间序列分析模型详细讲解

时间序列分析

时间序列也称动态序列，是指将某种现象的指标数值按照时间顺序排列而成的数值序列。

时间序列分析大致可分成三大部分，分别是描述过去、分析规律和预测未来。

本文主要包含常用的三种模型：

• 季节分解
• 指数平滑模型
• ARIMA模型

  季节分解

  时间序列的数值变化规律

  数值变化规律	代表字母	特点
  长期变动趋势	T	统计指标在相当长的一段时间内，受到长期趋势影响因素的影响，表现出持续上升或持续下降的趋势。
  季节变动趋势	S	指由于季节的转变使得指标数值发生周期性变动。一般以月、季、周为时间单位，不能以年作单位。
  周期变动规律（循环变动）	C	循环变动通常以若干年为周期，在曲线图上表现为波浪式的周期变动。最典型的周期案例就是市场经济的商业周期和的整个国家的经济周期。
  不规则变动（随机扰动项）	I	由某些随机因素导致的数值变化，不可预知、没有规律（在回归中又被称为扰动项）。

  一个时间序列往往是以上四类变化形式的叠加，四种变动与指标数值最终变动的关系可能是叠加关系，也可能是乘积关系。由于变动组合的不确定性，时间序列的数值变化才那么千变万化。

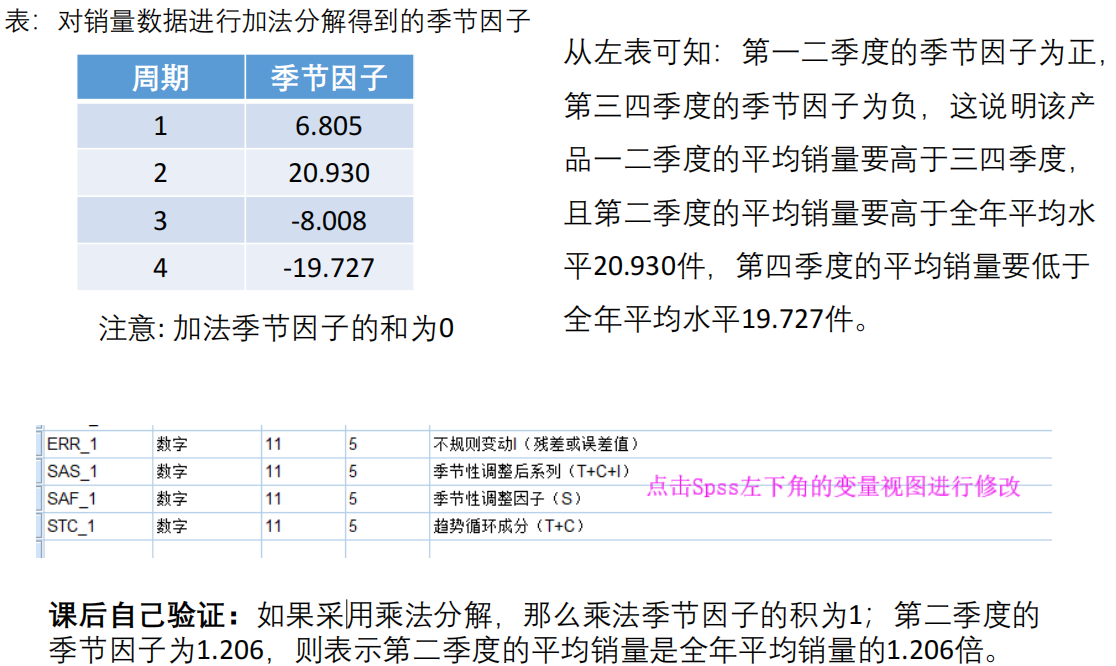
  • 如果四种变动之间是相互独立的关系，那么叠加模型可以表示为：Y = T + S + C + I
  • 如果四种变动之间存在相互影响关系，那么应该使用乘积模型：Y = T × S × C × T

    

    SPSS对数据预处理

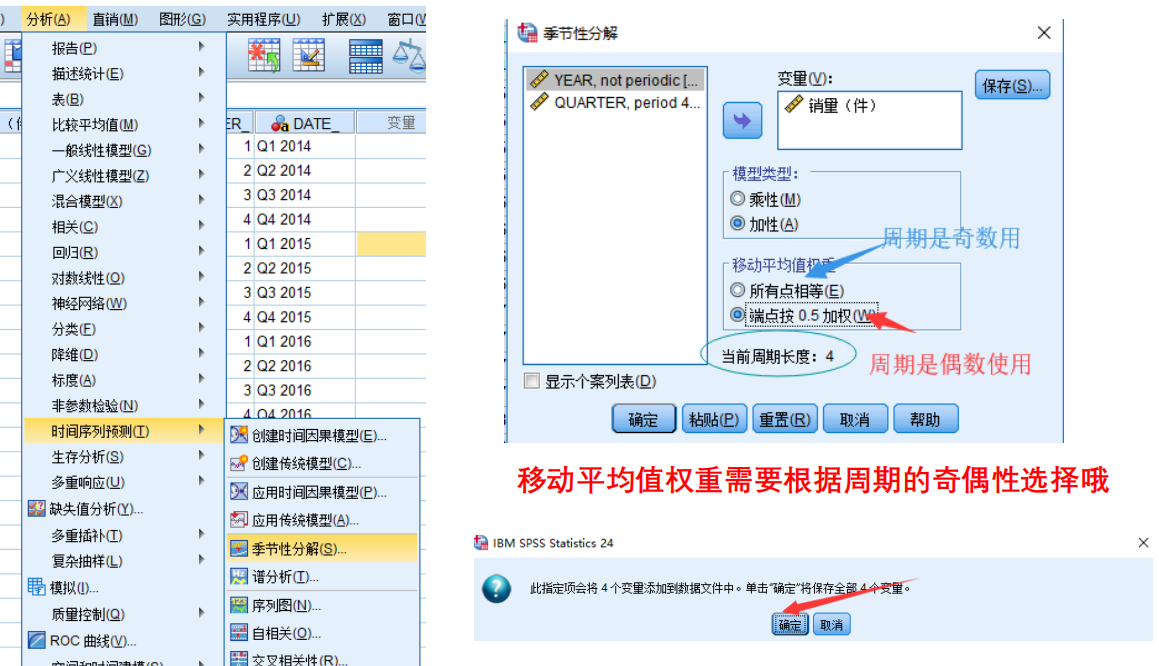
    顺序	方法	步骤
    1	处理时间序列中的缺失值	序列的中间位置：转换 —> 替换；缺失值序列两端：直接删除
    2	定义时间变量	数据 —> 定义日期和时间 —> 在“个案是”中选择合适的格式，并设置好起始时间
    3	绘制时间序列图（时序图）	分析 —> 时间序列预测 —> 序列图（“差异”选项即为进行几阶差分）

    SPSS季节性分解

    • 季节性分解

      

      • 结果解读

        

        • 绘制分解后的时序图

          

          时间序列分析的具体步骤

          1. 作时间序列图 —> SPSS软件解决
          2. 判断时间序列包含的变动成分
          3. 时间序列分解（有周期性且包含长期趋势、季节变动或循环变动）—> SPSS软件解决
             • 数据具有年内的周期性时才能使用时间序列分解，周期大于一年的不能够进行时间序列分解
             • 建立时间序列分析模型
             • 预测未来的指数指标

          建立时间序列分析模型

          SPSS专家模拟器可以帮助我们寻找最佳的拟合模型（指数平滑模型或ARIMA模型）。

          也即这部分如何选择，是由SPSS帮我们判断的。

          指数平滑模型

          名称	英文名称	使用条件	与之类似的ARIMA模型
          简单指数平滑法	Simple模型	不含趋势和季节成分	ARIMA（0，0，1）
          （霍特）线性趋势模型	linear trend	线性趋势、不含季节成分	ARIMA（0,2,2）
          阻尼趋势模型	Damped trend	线性趋势逐渐减弱且不含季节成分	ARIMA（1,1,2）
          简单季节性	Simple seasonal	含有稳定的季节成分、不含趋势	SARIMA（0,1,1）×（0,1,1)s
          温特加法模型	Winters’ additive	含有线性趋势和稳定的季节成分	SARIMA（0,1,0）×（0,1,1)s
          温特乘法模型	Winters’ multiplicative	含有线性趋势和不稳定的季节成分	不存在

          ARIMA模型

          模型	形式	说明
          ARIMA模型	ARIMA(p,d,q)	处理非季节性数据，亦称“差分自回归移动平均模型”
          SARIMA模型	SARIMA(p,d,q) (P,D,Q)m	模型形式前半部分为非季节部分，后半部分为季节部分

          ARIMA(p,d,q)模型 —— 差分自回归移动平均模型、SARIMA(Seasonal ARIMA)模型 ARIMA(p,d,q) (P,D,Q)m 前半部分为非季节部分，后半部分为季节部分。

          注意：

          • 模型选择：AIC和BIC准则（选小原则）

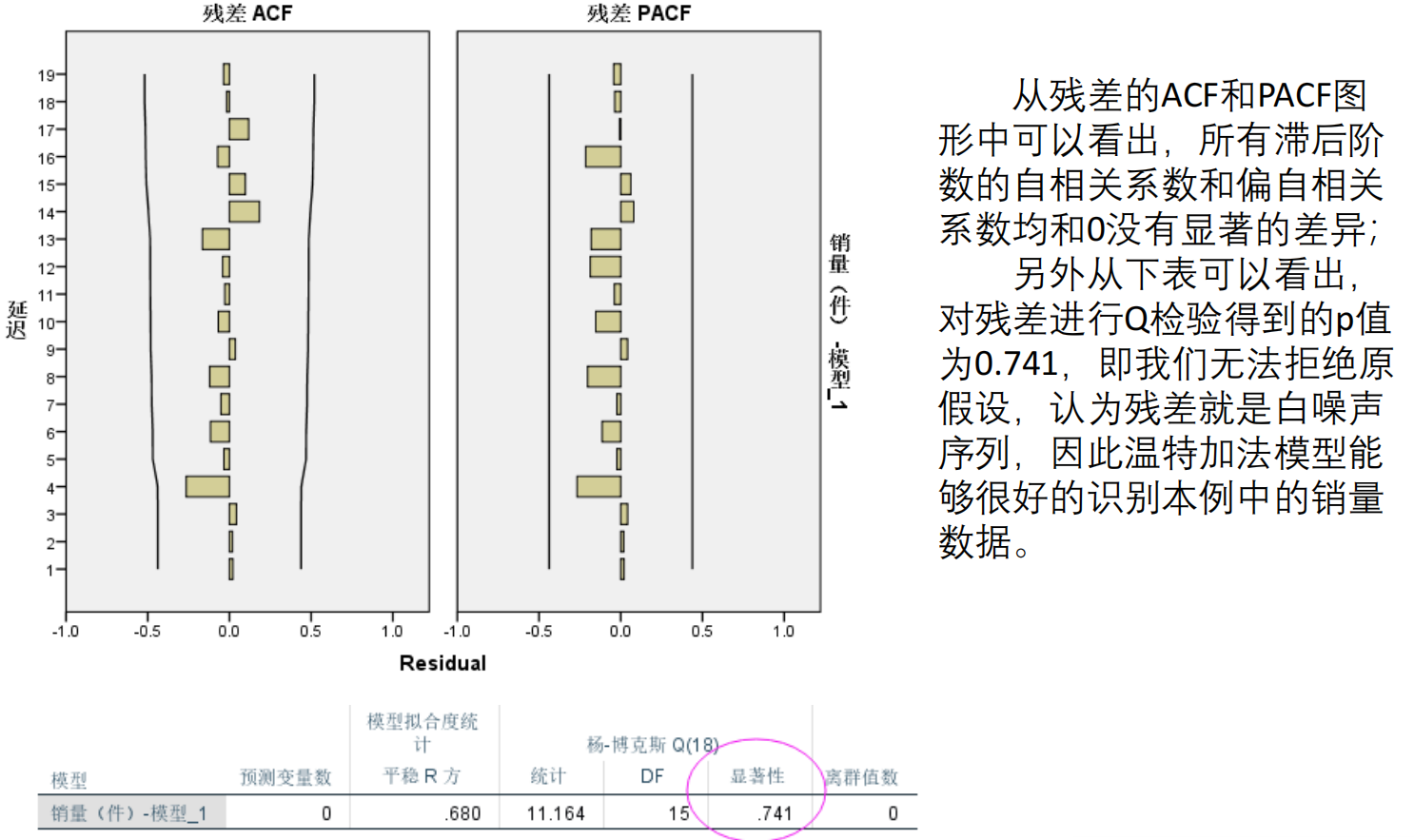
          • 残差自相关函数（ACF）、残差偏自相关函数（PACF），用来确定残差是否是白噪音

          • Q检验的显著性用于判断残差是否为白噪声：如果显著，则残差为白噪声，说明我们选取的模型能完全识别出时间序列数据的规律，即模型可接受。否则，需要对模型进行修订。

            时间序列分析解题步骤（论文写作）

            论文写作步骤

            1. 由于数据是完整的（或处理后），且为季度数据，因此可以做出其时间序列图。
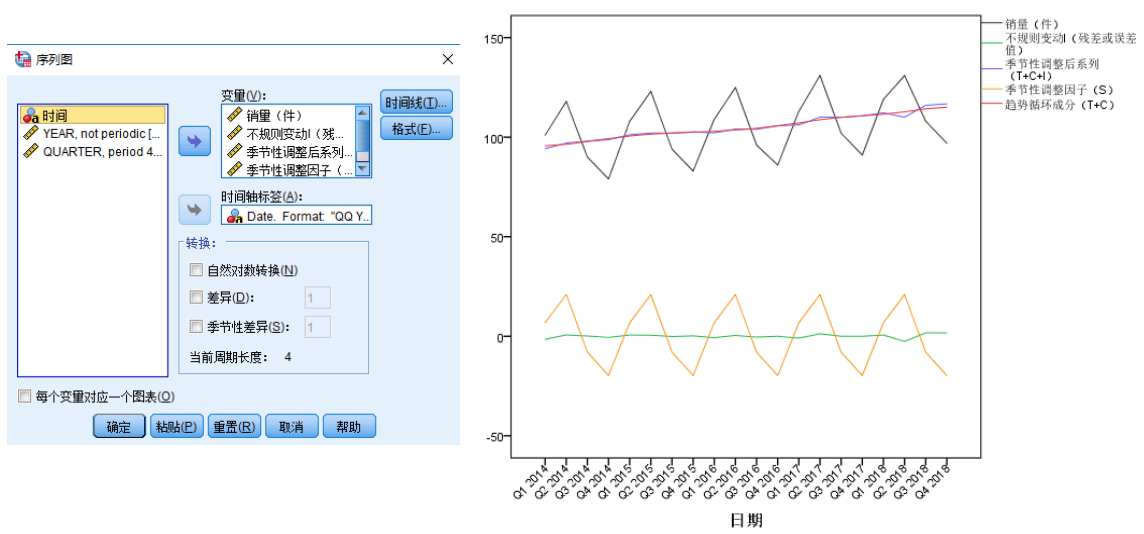
            2. 分析图中结果：从图中可以看出，销量数据具有向上的趋势，而且销量数据具有很明显的季节性波动。因此可以考虑使用时间序列分解。因为数据是平稳的，所以可以使用加法的时间序列分解，然后解释一波加法的时间序列分解。
            3. 使用SPSS的专家建模器（可以解释一波专家建模器），SPSS的专家建模器为我们选择出最合适的模型是温特加法模型，然后解释一波温特加法模型，SPSS为我们估计出的估计值也可以写在论文中。
            4. 白噪声检验：写入白噪声的输出图像，以及Q检验的结果（Q检验显著性＞0.05即可说明残差值就是白噪声）。
            5. 预测结果：我们考虑了95%的预测水平，在95%的预测水平下，写入SPSS输出的预测结果，95%的可能性落到哪与哪之间。加入预测图，可以使用SPSS输出的，也可以自己将数据处理后使用 分析 – 时间序列预测 – 序列图 作图。
            6. 汇报预测结果好坏：将平稳的R2、R2、标准化BIC放在论文中（平稳的R2、R2越大越好，标准化BIC越小越好）。

            例：

            如果SPSS选择了温特加法模型，在论文中就可以把温特加法模型的这部分数据写上：

            

            写入白噪声的输出图像，以及Q检验的结果，另外再加上右侧的文字。

            

            实际SPSS操作步骤

            1. 处理缺失值，生成时间变量
            2. 数据预处理（对数据进行描述性统计）
            3. 生成序列图分析
            4. 先使用专家模拟试探（先不去异常值），如果给出了温特斯加性之类的模型，说明时间序列分解的四种变动是叠加关系，之后可以进行季节性分解。
            5. 季节性分解：这时候可以将输出的季节因子在论文中展现，主要是分析一波哪个周期是正的，哪个周期是负的，哪个周期的绝对值最大、最小。
            6. 制作季节性分解序列图
            7. 可以对 季节性调整后序列 进行线性拟合，求出 R2 和SSE，然后去掉异常值再拟合一次，说明效果不佳，之后使用SPSS专家建模器。
            8. SPSS专家建模器：将专家检验得到的模型、模型拟合度、模型统计、离群值、残差ACF、PACF图像、预测结果图像等信息体现在论文中；将数据预测结果放在论文中，强调一下置信区间的置信度是95%。