二叉树详解(深度优先遍历、前序，中序，后序、广度优先遍历、二叉树所有节点的个数、叶节点的个数)

目录

一、树概念及结构(了解) 

1.1树的概念 

1.2树的表示 

二、二叉树概念及结构 

2.1概念 

2.2现实中的二叉树：

2.3数据结构中的二叉树：

2.4特殊的二叉树： 

2.5 二叉树的存储结构 

2.51 顺序存储： 

2.5.2 链式存储：

三、二叉树性质相关选择题练习 

四、二叉树的实现

4.1头文件：

4.2Test.c

4.3前序，中序，后序(深度优先遍历)

 4.4二叉树所有节点的个数

​编辑

4.5叶节点的个数

4.6层序遍历(广度优先遍历，使用队列)

一、树概念及结构(了解) 

1.1树的概念 

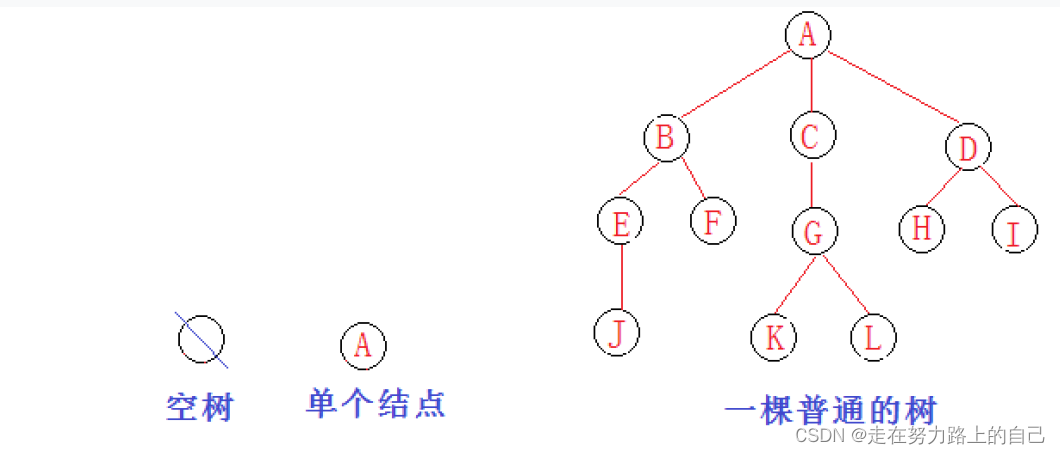
树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。把它

叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。
有一个特殊的结点，称为根结点，根节点没有前驱结点除根节点外，其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm，其中每一个集合Ti(1data = a[*pi]; ++(*pi); // 递归地创建左子树和右子树 root->left = CreatTree(a, pi); root->right = CreatTree(a, pi); return root; // 返回新创建的节点 }

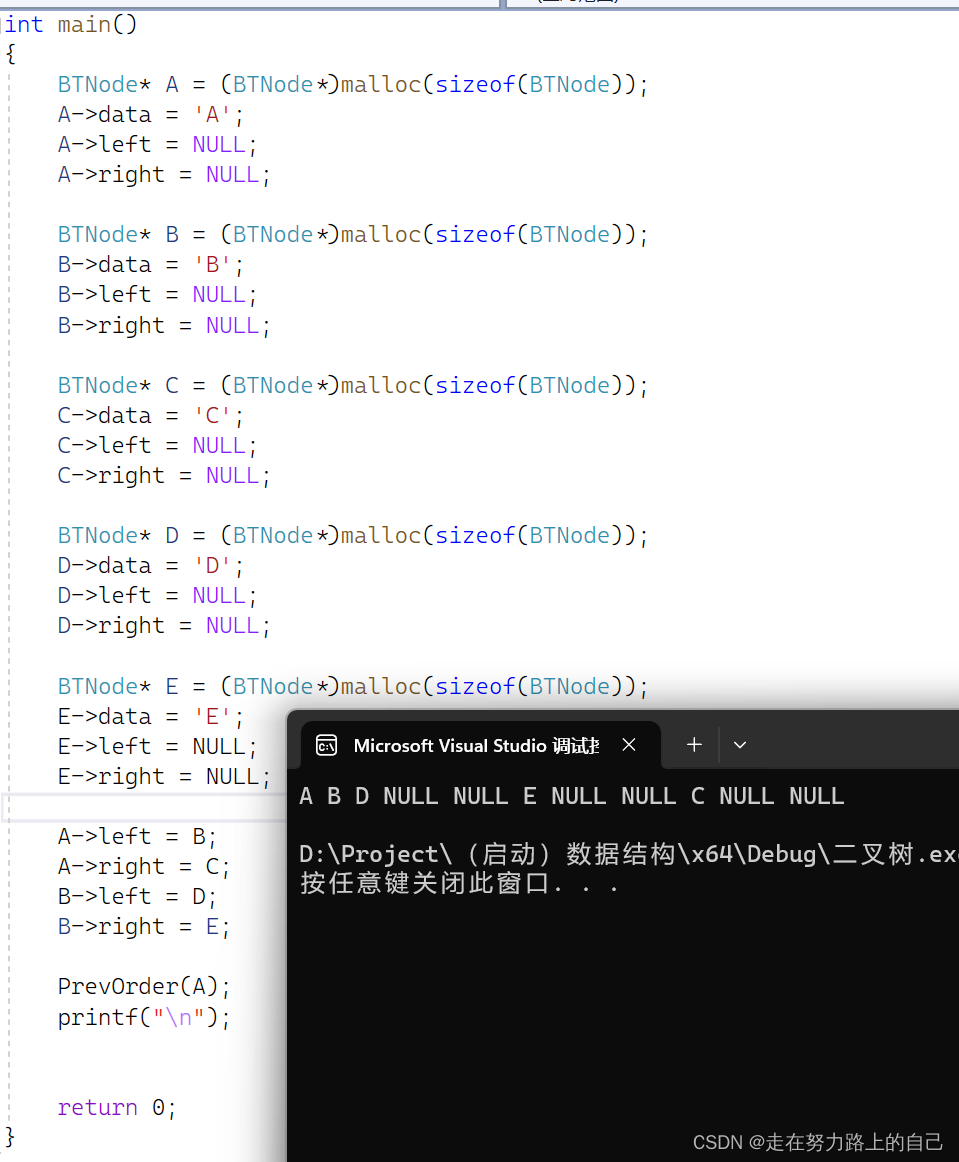
4.4前序，中序，后序(深度优先遍历)

// 先序遍历二叉树  
void PrevOrder(BTNode* root)
{
	// 如果当前节点为空，则打印"NULL"并返回  
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	// 访问当前节点的数据  
	printf("%c ", root->data);
	// 递归遍历左子树  
	PrevOrder(root->left);
	// 递归遍历右子树  
	PrevOrder(root->right);
}
// 中序遍历二叉树  
void InOrder(BTNode* root)
{
	// 如果当前节点为空，则打印"NULL"并返回  
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	// 递归遍历左子树  
	InOrder(root->left);
	// 访问当前节点的数据  
	printf("%c ", root->data);
	// 递归遍历右子树  
	InOrder(root->right);
}
// 后序遍历二叉树  
void PostOrder(BTNode* root)
{
	// 如果当前节点为空，则打印"NULL"并返回  
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	// 递归遍历左子树  
	PostOrder(root->left);
	// 递归遍历右子树  
	PostOrder(root->right);
	// 访问当前节点的数据  
	printf("%c ", root->data);
}

 4.4二叉树所有节点的个数

//方法一:定义全局变量(不推荐)
// 全局变量，用于记录树的大小（节点数）  
// 注意：使用全局变量通常不是好的做法，应该尽量避免  
int size = 0;  
  
// 计算二叉树的大小（节点数）
void TreeSize(BTNode* root)  
{  
	// 如果节点为空，则不计算大小，直接返回  
	if (root == NULL)  
	{  
		return; // 在 void 函数中这样写是可以的，但如果是 int 类型函数则需要返回一个整数值  
	}  
	else {  
		// 节点非空，增加 size 的计数  
		++size;  
	}  
  
	// 递归计算左子树的大小  
	TreeSize(root->left);  
	// 递归计算右子树的大小  
	TreeSize(root->right);  
	
}

方法二:传址调用

// 定义TreeSize函数，用于计算二叉树的大小（节点数）  
// 参数：root - 指向二叉树根节点的指针；psize - 指向一个整数的指针，用于存储节点数  
void TreeSize(BTNode* root, int* psize)  
{  
	// 如果根节点为空（即树为空），则直接返回，不执行任何操作  
	if (root == NULL)  
	{  
		return;  
	}  
	else // 如果根节点不为空（即树非空）  
	{  
		// 通过解引用psize指针来递增其指向的整数值，表示当前节点被计数  
		++(*psize);  
	}  
  
	// 递归调用TreeSize函数来计算左子树的大小  
	TreeSize(root->left, psize);  
	// 递归调用TreeSize函数来计算右子树的大小  
	TreeSize(root->right, psize);  
}

方法三:递归、分治思想:

否则，返回左子树节点数 + 右子树节点数 + 1（当前节点）

int TreeSize(BTNode* root)
{
    // 如果树为空（即根节点为NULL），则返回0  
    // 否则，返回左子树节点数 + 右子树节点数 + 1（当前节点）
    return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

4.6叶节点的个数

int LeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	if (root->left == NULL && root->right == NULL)
		return 1;
	return TreeSize(root->left) + TreeSize(root->right);
}
// 计算二叉树中叶子节点的数量（但存在错误）  
int LeafSize(BTNode* root)  
{  
    // 如果当前节点为空，说明不是叶子节点，返回0  
    if (root == NULL)  
        return 0;  
  
    // 如果当前节点既没有左子树也没有右子树，那么它是一个叶子节点，返回1  
    if (root->left == NULL && root->right == NULL)  
        return 1;  
  
    // 递归计算左子树和右子树中的叶子节点数量，并返回它们的和
    return TreeSize(root->left) + TreeSize(root->right); 
}

4.7层序遍历(广度优先遍历，使用队列)

这是使用的队列的代码

//队列初始化
void QueueInit(Queue* pq)
{
	assert(pq);
	pq->head = pq->tail = NULL;
}
//队列的销毁
void QueueDestory(Queue* pq)
{
	assert(pq);
	QNode* cur = pq->head;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}
	pq->head = pq->tail = NULL;
}
// 队尾入
void QueuePush(Queue* pq, QDataType x)
{
	assert(pq);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	newnode->data = x;
	newnode->next = NULL;
	if (pq->tail == NULL)
	{
		pq->head = pq->tail = newnode;
		//表示这是第一个节点
	}
	else
	{
		pq->tail->next = newnode;
		//tail的后面加上新节点
		pq->tail = newnode;
		//再让tail指向newnode
	}
}
// 队头出
void QueuePop(Queue* pq)
{
	
	assert(pq);
	assert(pq->head);
	// 1、一个
	// 2、多个
	if (pq->head->next == NULL)
	{
		free(pq->head);//释放队头的空间
		pq->head = pq->tail = NULL;
		//队列为空
	}
	else
	{
		QNode* next = pq->head->next;
		//存储队头下一个节点的空间
		free(pq->head);
		//释放队头的空间
		pq->head = next;
		//让队头指向之前队头的下一个节点
	}
}
//队头数据
QDataType QueueFront(Queue* pq)
{
	assert(pq);
	assert(pq->head);
	return pq->head->data;
}
//队尾数据
QDataType QueueBack(Queue* pq)
{
	assert(pq);
	assert(pq->head);
	return pq->tail->data;
}
//队列数据个数
int QueueSize(Queue* pq)
{
	assert(pq);
	int size = 0;
	QNode* cur = pq->head;
	while (cur)
	{
		++size;
		cur = cur->next;
	}
	return size;
}
//判断队列是否为空
bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->head == NULL;
}

// 层序遍历二叉树  
void LevelOrder(BTNode* root)  
{  
    // 定义一个队列q  
	Queue q;  
    // 初始化队列  
	QueueInit(&q);  
    // 如果根节点不为空  
	if (root)  
	{  
        // 将根节点入队  
		QueuePush(&q, root);  
	}  
    // 当队列不为空时循环  
	while (!QueueEmpty(&q))  
	{  
        // 取出队列的队首元素，但不从队列中移除  
		BTNode* front = QueueFront(&q);    
  
        // 从队列中移除队首元素  
		QueuePop(&q);  
        // 访问队首元素的数据  
		printf("%c ", front->data);  
  
        // 如果队首元素有左子节点，将左子节点入队  
		if (front->left)  
		{  
			QueuePush(&q, front->left);  
		}  
        // 如果队首元素有右子节点，将右子节点入队  
		if (front->right)  
		{  
			QueuePush(&q, front->right);  
		}  
	}  
    // 销毁队列，释放其占用的资源  
	QueueDestory(&q); 
}

​​​​​​​​​​​​​​

新年第一篇！！！

祝大家新年快乐

看到这里了还不给博主扣个：

⛳️ 点赞☀️收藏 ⭐️ 关注！

你们的点赞就是博主更新最大的动力！

有问题可以评论或者私信呢秒回哦。