算法与程序的区别与联系
.程序不一定满足有限性。比如,只要整个系统不被破坏,它就永远不会停止。即使没有作业要处理,它仍然在动态等待。程序中的指令必须是机器可执行的,但算法中的指令没有这样的限制。算法代表了问题的解决方案,而程序则是算法在计算机上的具体实现。算法是对解决特定问题的步骤的描述,是有限的指令序列。程序是一系列执行操作以实现预期目的的语句和指令。一般来说,一些算法是解决问题的思路,而程序是可以编写来解决这些问题的具体代码。算法往往包含重复的步骤和一些逻辑判断。可以理解为数据结构和算法组成了可执行程序。硬件、软件、算法和编程有什么区别?
(1).程序不一定满足有限性。 比如,只要整个系统不被破坏,它就永远不会停止。 即使没有作业要处理,它仍然在动态等待。 因此,操作系统不是算法。
(2)。 程序中的指令必须是机器可执行的,但算法中的指令没有这样的限制。
(3)。 算法代表了问题的解决方案,而程序则是算法在计算机上的具体实现。 如果用编程语言描述算法,那么它就是程序。
算法与程序的区别与联系
算法和程序的区别在于:
(1)两者的定义不同。 算法是对解决特定问题的步骤的描述,是有限的指令序列。 程序是一系列执行操作以实现预期目的的语句和指令。
一般来说,一些算法是解决问题的思路,而程序是可以编写来解决这些问题的具体代码。 算法没有语言界限。 他只是一个想法。 实现同一个算法,不同语言编写的程序会有所不同。
(2)两者的书写规定不同。 程序必须用规定的编程语言编写,而算法是任意的。 算法是解决问题的一系列明确的指令,即对于一定的标准化输入,能够在有限的时间内得到所需的输出。 算法往往包含重复的步骤和一些逻辑判断。
简单算法示例:求1*2*3*4*5
步骤一:先求1*2,得到结果2。
步骤2:将步骤1得到的乘积2乘以3得到结果6。
步骤3:将步骤2得到的乘积6乘以4得到结果24。
步骤4:将步骤3得到的乘积24乘以5,得到最终结果120。
算法与程序的联系:
算法和程序都是有限的指令序列,但程序是算法,算法不一定是程序。 程序=数据结构+算法。 算法的主要目的是为人们提供对工作流程和执行步骤的可读理解。 数据结构和算法必须通过程序来实现,然后才能被计算机系统执行。 可以理解为数据结构和算法组成了可执行程序。
扩展信息
算法的要素:
1.操作和数据对象的操作:计算机可以执行的基本操作以指令的形式描述。 计算机系统能够执行的所有指令的集合就成为计算机系统的指令系统。 计算机的基本计算和操作分为以下四类:
1、算术运算:加、减、乘、除等运算。
2、逻辑运算:OR、AND、NOT等运算。
3、关系运算:大于、小于、等于、不等于等运算。
4、数据传输:输入、输出、赋值等操作。
2.算法控制结构:算法的功能结构不仅取决于所选择的操作,还与操作之间的执行顺序有关。
参考:百度百科算法
算法和程序有什么区别
算法是解决问题的步骤; 程序是算法的代码实现
算法依靠程序来完成功能; 程序需要算法作为灵魂
算法与程序的关系
算法和程序:
(1).程序不一定满足有限性。 比如,只要整个系统不被破坏,它就永远不会停止。 即使没有作业要处理,它仍然在动态等待。 因此,操作系统不是算法。
(2)。 程序中的指令必须是机器可执行的,但算法中的指令没有这样的限制。
(3)。 算法代表了问题的解决方案,而程序则是算法在计算机上的具体实现。 如果用编程语言描述算法,那么它就是程序。
什么是算法? 其五个特点是什么? 算法和程序之间是什么关系?
算法是指对问题解决方案的准确、完整的描述。 它是一系列解决问题的明确说明。 算法代表了描述解决问题的策略机制的系统方法。
一个算法应该具有以下五个重要特征:
有限性
算法的有限性意味着该算法必须能够在执行有限数量的步骤后终止;
确定性
算法的每一步都必须明确定义;
输入
算法有0个或多个输入来描述操作对象的初始情况。 所谓0输入是指算法本身设定初始条件;
输出
算法具有一个或多个反映输入数据处理结果的输出。 没有输出的算法是没有意义的;
效力
算法中执行的任何计算步骤都可以分解为基本的可执行操作步骤,即每个计算步骤都可以在有限的时间内(也称为有效性)完成。
算法和程序的关系是:
算法是程序的灵魂。 一个程序需要实现一个特定的功能。 实现它的算法可以有很多种,所以算法的质量决定了程序的质量。
程序是遵循一定规则并为完成指定工作而编写的代码。 有一个经典的方程式阐明了什么是程序:程序=算法+数据结构+编程方法+语言工具和环境。
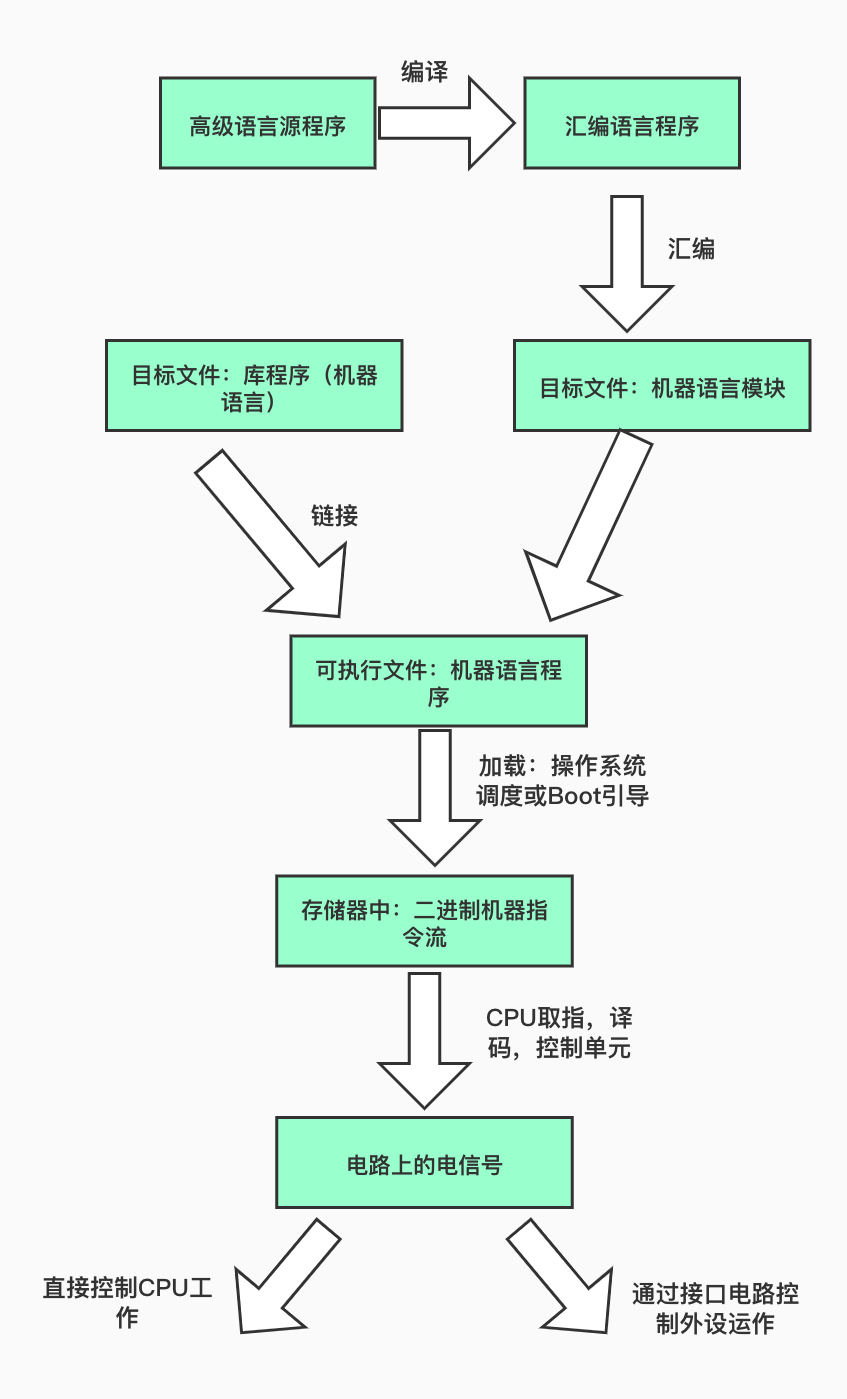
硬件、软件、算法和编程有什么区别?
一般来说,软件是程序员为计算机系统编写的程序,是计算机系统的上层。 硬件是一个复杂的电路系统,是计算机系统的底层。 软件工程师的工作与编程相关,硬件工程师的工作与电路设计、编码等相关。
从历史上看,计算机的原型比软件早几个世纪出现。
电子计算机的出现与苏格兰数学家布尔和现代信息学之父美国香农密不可分。 布尔以其非凡的智慧发明了他的布尔代数或布尔逻辑,使代数脱离了数的概念而变得更加抽象。 布尔代数中的操作数不是数字,而是集合(类),并且一个类仅代表一个类。 事物的组,后来称为集合。 古希腊人认为逻辑是分析语言以追求真理的手段,因此被认为是一种哲学。 所以布尔不仅用数学方法将逻辑从哲学中分离出来,而且还为电子计算机的出现奠定了基础。 遗憾的是,在19世纪,没有人将布尔代数中的AND和OR与电路中的串并联开关联系起来。 没有人意识到布尔代数可以直接用电路来实现。 直到20世纪30年代才被发现。 主要贡献者是现代信息学之父香农。 香农在1938年写于麻省理工学院的著名硕士论文《继电器和开关电路的符号分析》中详细阐述了这个问题。
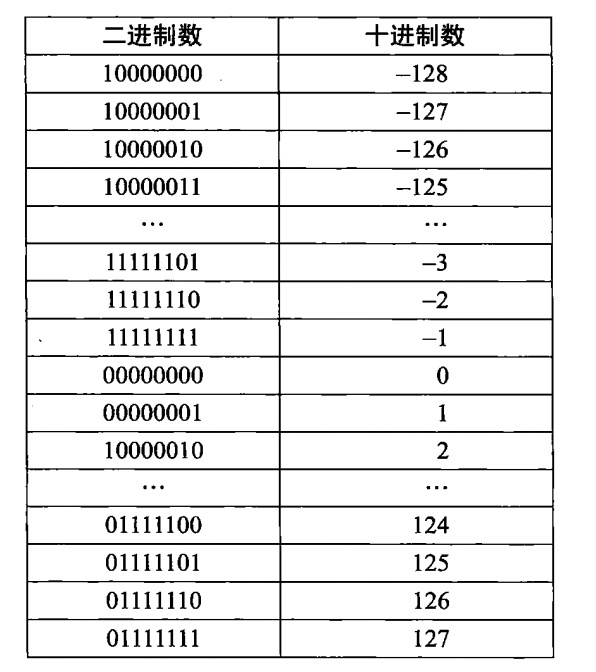
现代电子计算机完成的加法和减法运算都是由逻辑器件组成的电路来完成的。 计算机使用二进制数进行工作。 二进制数 0 和 1 代表逻辑设备中的中断和路径。
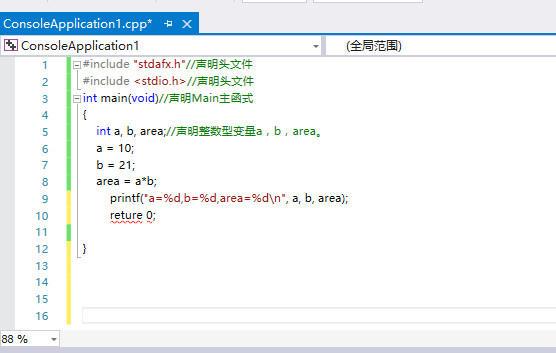
软件的本质是计算机系统(硬件)的编程。 软件通常用高级语言编程。 程序员编写的程序经过IDE编译、链接后用电烧录到计算机系统的程序寄存器中,但存储在程序寄存器中。 里面是机器码,很多01010111的代码。 这里我就以微控制器(microcontroller)的工作原理为例来说明后面它是如何工作的。 单片机执行指令时,首先从程序存储器中读取指令,送入指令寄存器存储,然后送入指令译码器译码。 译码结果送至时序控制逻辑电路,由定时器控制逻辑产生各种时序信号和控制信号。 然后传送到单片机的各个部件进行相应的操作。 执行程序意味着一遍又一遍地重复这个过程。
简而言之,我认为计算机相当复杂。
算法和程序有哪些相同点和不同点?
算法和程序:
(1).程序不一定满足有限性。 比如,只要整个系统不被破坏,它就永远不会停止。 即使没有作业要处理,它仍然在动态等待。 因此,操作系统不是算法。
(2)。 程序中的指令必须是机器可执行的,但算法中的指令没有这样的限制。
(3)。 算法代表了问题的解决方案,而程序则是算法在计算机上的具体实现。 如果用编程语言描述算法,那么它就是程序。
MQ算术编码器原理与实现
郭庆
北京邮电大学信息与通信工程学院 北京 (100876)
电子邮件:
摘要:在JPEG2000标准中,MQ算术编码是熵编码的主要部分。 MQ 算术编码器是一种基于上下文的自适应二进制算术编码器。 它基于上下文方便信源去相关,利用条件交换和概率估计状态机中的贝叶斯学习过程实现符号概率模型自适应过程,并利用比特填充技术解决中的进位问题编码,这是一种高效的方法。 物理上可实现的压缩编码算法。 本文从算术编码的基本原理出发,详细分析JPEG2000标准提供的MQ编码器的编码原理,以及编码过程。 使用C语言编程实现JPEG2000标准要求的MQ算术编码器,并分析MQ算术编码器中上下文引入对压缩效率的影响。
关键词:JPEG2000; 算术编码; MQ算术编码器
CLC分类号:TN911.21
1 简介
随着多媒体技术的不断应用和发展,图像压缩需要更高的性能和新的功能。 为了满足特殊领域对静态图像编码的需要,JPEG2000作为新的标准正在不断发展。 这个新标准更加关注图像的可扩展表示[1]。
算术编码是一种变长信源编码技术,其优异的性能使其在多媒体领域得到越来越广泛的应用[2]。 在JPEG2000标准中,提高图像压缩性能的关键技术之一是MQ算术编码。 MQ算术编码器是一种基于上下文的自适应二进制算术编码器。 它继承了IBM的ABIC(自适应双层图像压缩)中Q编码器的无乘逼近和位缓存策略,并添加了条件交换和概率估计状态机中的贝叶斯学习过程,是一种高效的物理上可实现的压缩编码算法,具有重要的研究价值。
2. 算术编码
2.1 编码原理简述
算术编码是一种非阻塞编码。 编码过程中,源符号序列不断进入编码器,通过编码器的运算得到连续的输出。 通常算术编码是将源符号序列映射为代码序列。 这样的代码序列有时也称为代码字。 算术编码的本质是将源信息序列映射到[0,1)区间中的子区间。 这个映射是一一对应的,保证解码唯一,然后取子区间。 由点表示的值用作码字。 只要代码长度合适,就可以保证唯一可译。 当源序列长度足够大时,每个源符号的平均码长接近于源的熵[2]。
虽然它的编码效率非常高,但仍然存在缺陷。 首先,它的运算需要精确的实数加法和乘法,这在有限精度的计算机上很难实现。 正是由于这个原因,算术编码与其实际应用相差了近二十年。 直到Rissanen和Pasco分别提出先进后出算法和先进先出算法,从而证明算术编码可以用有限精度的处理技术来近似。 Rubin吸收了两种算法的精华,使用有限精度寄存器,讨论了通用算术编码的实现方法。 在此基础上,Witten、Neal和Cleary进一步完善,给出了完整的C语言程序。
算术编码的另一个缺点是编码速度太低。 这是因为编码迭代过程包含整数乘法和除法运算,这对软件执行和硬件设计非常不利。
为此,Langdon和Rissanen提出了一种利用移位和加法实现二进制算术编码的方法,并成功地将其应用于黑白二值图像的压缩编码。 二进制算术编码是一个逐步的编码和解码过程。它不需要
为了等到待编码的序列完全输入到编码器中,可以在输入序列的同时输出编码后的码字。 它还解决了算术编码的准确性问题。
2.2 二进制算术编码
如前所述,二进制算术编码是一个不断增长的编码和解码过程。 当序列进入编码器时即可获得编码输出,无需等待所有序列完全进入编码器。
以消息“cacbad”为例说明编码过程。 一开始整个区间是一个半开半闭的区间R0=[0,1),仍然按照每个符号的概率分解为四部分:[0.5, 0.62), (0.62, 0.70) ,[0.70,0.86),[0.86,0.9)来表示a,b,c,d区间。 计数器 Count 最初设置为 0。
第一个符号是c,区间R1=[0.5,0.9)完全属于[0.5,1)。 是情况2,所以编码输出为1bit:1。同时根据情况2,将区间大小改为R2=[0.0,0.8)。由于Count=0,所以不输出码字。
第二个符号为a,区间调整为R3=[0.0,0.24)。 由于整个区间属于前半部分,即情况1,因此输出1bit:0,区间调整为R4[0.0,0.48)。 还是属于上半场。 继续输出0,调整间隔为R5=[0.0,0.96)。
第三个符号为c,区间调整为R6=[0.48,0.864)。 不需要输出任何码字,也不需要调整间隔。 第四个符号是b。 区间调整为R7=[0.5952,0.672),属于情况2,输出1,调整区间R8=
[0.1904,0.344)。 情况1,输出为0,调整区间为R9=[0.3808,0.688)。
此时,该区间属于情况3,因此我们将计数器加1:Count=1,并将区间调整为R10=[0.2616,0.876)。
第五个符号为a,区间调整为R11=[0.2616,0.44592)。 情况1时,输出0,调整间隔R12=[0.5232,0.89184)。 此时计数器大于0,因此输出计数器值为1bit:1。 新的区间为情况1,因此输出为1,调整为R13=[0.0464,0.78368)。
最后一个符号为d,区间调整为R14=[0.709952,0.78368)。 情况2,输出1,调整为R15=[0.419904,0.56736)。 至此我们结束编码,可以使用该区间内的任意值作为码字输出。 我们取0.5,那么二进制表示就是0.1000000b,你可以添加任意多个0,以满足位数要求。
因此,作为唯一可解码的编码,编码过程中输出的码字与最终区间内的任意值进行组合,得到的字符串就是实际的16位编码:1001 0011 1100 0000。可以看出,前9位是增长编码过程的输出,从区间中选择后7位并与前9位组合形成16位编码。
详细编码流程如图1所示:
图1 “cacbad”二进制算术编码流程图
3、MQ算术编码器原理
3.1 MQ编码器结构
JPEG2000标准中MQ编码器的结构如图2所示。编码器输入由待编码比特D和上下文向量CX组成,它们由EBCOT(嵌入式位平面失真率优化编码)成对生成。 CX是位平面编码中基于邻域相关性总结的概率统计模型,共有19种类型。 也就是说,对于不同的CX,符号概率是不同的。
图2 MQ编码器结构图
3.2 递归区间划分和编码逼近
具有递归概率区间划分的ELIAS编码是二进制算术编码的基础[3]。 算术编码器首先根据符号概率将符号分为高概率符号MPS和小概率符号LPS。 划分间隔时,LPS间隔先于MPS间隔。 如图2所示:
图3 MQ编码器编码区间示意图
当对MPS进行编码时,LPS子间隔间距被添加到编码串中。 因此,在对每一位进行编码时,必须提前知道LPS子区间的大小和MPS的代表符号。 编码过程就是对输入的每一位进行判断,不断改变编码串C的值,使其指向当前区间的底部。 编码过程使用二进制小数加法而不是整数数字的串行加法。 概率较大的二进制比特可以用小数比特进行编码,从而减少编码位数,达到压缩的效果。
假设A是当前区间,Qe是LPS的估计概率。 那么要精确划分区间,必须满足以下公式:
MPS子区间区间=A-(Qe*A) (1)
LPS子区间间隔=Qe*A (2)
为了避免硬件难以实现的乘法运算,在JPEG2000中改为使用以下公式来避免乘法运算:
MPS子区间区间=A-(Qe*A) (3)
LPS子区间间隔=Qe*A (4)
编码时简化运算,直接用小概率符号概率Qe代替LPS区间长度Qe*A,省去乘法运算。 当对MPS进行编码时,Qe被添加到编码字符串的值上,并且区间被减小到A-Qe。 LPS编码时,编码串C保持不变,间隔缩小为Qe。 然后根据需要对A和C进行归一化,使A落在0.75到1.5的区间内(原来的全概率区间为[0,1.5),0.75为中点值)[4]。 相应的整形表示是保持A大于0x8000。 如果小于该值,则寄存器 C 和 A 通过重整化过程左移。
由于区间划分采用这样的近似,所以在某个点LPS的概率可能大于MPS。 例如,当A值为0.75,Q为0.5时,MPS的概率为A-Qe=0.25。 为了避免这种反转现象,当LPS的间距大于MPS的间距时,它们被互换。
3.3 自适应模型
上述算术编码过程基于每个符号的已知概率。 只有知道每个符号的概率,才能据此划分概率区间。 在实际应用中,必须通过概率统计模型来获得每个符号的概率。 模型提供了编码符号的概率,编码算法使用相应的概率对符号进行编码。 JPEG2000 中的算术编码使用基于上下文向量的自适应模型。
一方面,符号概率的确定是一个自适应过程。 利用概率转移有限状态机根据输入消息符号实时调整符号概率。 另一方面,它的状态转移是一个基于上下文的过程。 编码器的输入不仅是消息序列D,还有上下文CX。 对于同一个消息D,如果其上下文CX不同,则对应的符号概率不一定相同。 必须读取CX当前状态的符号概率来确定消息的符号概率,同时决定是否转移到下一个状态。 标准提供了符号概率的状态转换表,共有47种状态。
3.4位填充技术
在二进制算术编码中,由于编码过程采用了增长传输技术,因此必须保证当前编码字节中存在进位时,不会影响编码器已经输出的字节。 MQ算术编码器采用位填充技术来解决进位问题[5]。
位填充技术的原理是,当编码中出现进位,导致缓冲区中输出的前一个字节溢出时,进位标志将作为当前字节编码的一部分,而不是添加到前一个码字中。
只有前一个码字为0xff时才会出现这种情况。 同时,为了方便解码,当前一个字节为0xfe,当前字节出现进位,导致前一个字节变成0xff时,仍然输出当前字节进位标志0作为编码。 这样,解码时,每当码字为0xff时,就会根据进位标志处理下一个码字的第一位。
4. MQ算术编码器实现及结果分析
4.1 编码器流程
图4 MQ编码器整体流程图
整体流程如上图4所示。 首先初始化编码器INTENC,然后读入上下文CX和要编码的字D,开始编码ENCODE。 直到编码结束,通过FLUSH过程清零寄存器,完成编码。
ENCODE 流程如下图 5 所示。 编码时,判断D是0还是1,如果是0,则将代码0编码为CODE0,如果为1,则将代码1编码为CODE1。
图5 ENCODE流程图
编码CODE0时,判断0是否为高概率符号。 如果是,则执行高概率符号编码CODEMPS,否则执行小概率符号编码。 CODE1编码类似。 该过程如图6和图7所示。
图6 CODE0流程图
图7 CODE1流程图
4.2 结果与分析
首先,我们检查未引入上下文 CX 时的压缩性能。 上下文生成时只要只生成一个上下文CX(0),该信息源就相当于不引入上下文的单符号独立随机信息源。 0符号概率时的压缩比为70%。 引入context后,压缩率接近68%,性能得到提升。
由于测试的片源没有经过JPEG2000预处理步骤,所以这个压缩率只能提供一定的参考。
5 结论
本文给出了MQ算术编码器的原理和实现过程,并用一个简单的模型初步探讨了上下文CX在编码中的作用。 要进行更深入的研究,必须对JPEG2000编码的其他模块进行进一步的研究和分析,了解JPEG2000中CX的生成机制,将前面的模块与算术编码器结合起来,分析其性能。
参考
[1]
[2]
[3]
[4]王芳,王伟。 JPEG2000图像压缩标准及其应用[J]. 光盘技术。 第 1 期,2006 年,1:57-59。 田宝玉. 工程信息论[M]. 北京邮电大学出版社. 2004:108-116。 李文斌,朱红. JPEG2000算术编码及其FPGA设计研究[J]. 遥测和远程控制。 第26卷,2005年,5:38~40。 金丽. 图像压缩:JPEG 2000 的数学[J].现代信号处理。 第 46 卷,
2003:185-221
[5] Tinku,Acharya,Ping-Sing,Tsai。 JPEG2000图像压缩标准:概念[J]、算法与
VLSI 架构。 约翰·威利父子公司,2004:30~195。
MQ算术编码原理及实现
郭庆
北京邮电大学(100876)
抽象的
MQ算术编码是熵编码中最重要的部分。 MQ算术编码是一种基于上下文的自适应二进制算术编码器。 它基于上下文以提高编码效率。 本文首先阐述了算术编码的理论,然后进一步阐述了二进制算术编码的理论以及如何实现有限精度算术编码器的实际应用。 关键词:JPEG2000算术编码 MQ-coder